【题目】已知点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=﹣3x+b上,则y1,y2,y3的值的大小关系是( )
A. y1>y2>y3 B. y1<y2<y3 C. y3>y1>y2 D. y3<y1<y2
参考答案:
【答案】A
【解析】∵直线y=3x+2,k=3<0,
∴y随x的增大而减小,
又∵2<1<1,
∴y1>y2>y3.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD.(尺规作图,不写作法,保留作图痕迹)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 0 既不是单项式也不是多项式
B. ﹣x2yz 是五次单项式,系数是﹣1
C. 3x2﹣3+5xy2 的常数项是 3
D. 多项式是整式
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,如果斜边上的中线CD=4cm,那么斜边AB=________ cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(a+1)2+|b﹣2|=0,求a2000b3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b的图象只经过第一、二、三象限,则( )
A. k<0,b>0 B. k>0,b>0 C. k>0,b<0 D. k<0,b<0
-
科目: 来源: 题型:
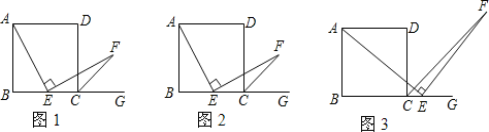
查看答案和解析>>【题目】数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F,求证:AE=EF.
经过思考,小明展示了一种正确的解题思路:在AB上截取BM=BE,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立。你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由。
相关试题

