【题目】如图,抛物线y=-![]() +
+![]() +4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
+4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
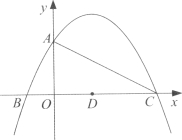
(1)点A的坐标为_______ ,点C的坐标为_______ ;
(2)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何值时,相应的点P有且只有2个?
参考答案:
【答案】(1)、A(0,4) C(8,0);(2)、![]() (0,4)、
(0,4)、![]() 、
、![]() (8-2
(8-2![]() ,
,![]() );(3)、S=16.
);(3)、S=16.
【解析】
试题分析:(1)、根据x=0和y=0分别求出点A和点C的坐标;(2)、首先求出点D的坐标,CD的长度和直线AC的解析式,然后分DE=DC,DE=EC和DC=EC三种情况分别求出点E的坐标;(3)、首先设出点P和点Q的坐标,然后列出面积的函数关系式,然后进行求解.
试题解析:(1)、A(0,4) C(8,0)
(2)、易得D(3,0),CD=5, 设直线AC对应的函数关系式为y=kx+b,则:![]()
解得: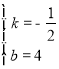 ; ∴y=-
; ∴y=-![]() x+4;
x+4;
①当DE=DC时,
∵OA=4,OD=3, ∴DA=5, ∴![]() (0,4);
(0,4);
②过E点作EG⊥x轴于G点,
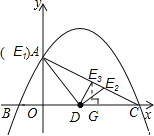
当DE=EC时,由DG=![]() ,
,
把x=OD+DG=3+![]() =
=![]() 代入到y=-
代入到y=-![]() x+4,求出y=
x+4,求出y=![]()
可得![]() ;
;
③当DC=EC时,如图,过点E作EG⊥CD, 则△CEG∽△CAO,
∴![]() ,又OA=4,OC=8,则AC=4
,又OA=4,OC=8,则AC=4![]() ,DC=EC=5, ∴EG=
,DC=EC=5, ∴EG=![]() ,CG=2
,CG=2![]() ,
,
∴![]() (8-2
(8-2![]() ,
,![]() );
);
综上所述,符合条件的E点共有三个:![]() (0,4)、
(0,4)、![]() 、
、![]() (8-2
(8-2![]() ,
,![]() )
)
(3)、如图,过P作PH⊥OC,垂足为H,交直线AC与点Q;
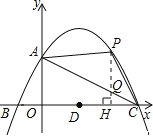
设P(m,-![]()
![]() +
+![]() m+4),则Q(m,-
m+4),则Q(m,-![]() m+4).
m+4).
①当0<m<8时,
PQ=(-![]()
![]() +
+![]() m+4)-(-
m+4)-(-![]() m+4)=-
m+4)=-![]()
![]() +2m,
+2m,
S=![]() +
+![]() =
=![]() ×8×(-
×8×(-![]()
![]() +2m)=-
+2m)=-![]() +16, ∴0<S≤16;
+16, ∴0<S≤16;
②当-2≤m<0时,
PQ=(-![]() m+4)-(-
m+4)-(-![]()
![]() +
+![]() m+4)=
m+4)=![]()
![]() -2m,
-2m,
S=![]() -
-![]() =
=![]() ×8×(
×8×(![]()
![]() -2m)=
-2m)=![]() -16,
-16,
∴0<S<20;
∴当0<S<16时,0<m<8中有m两个值,-2<m<0中m有一个值,此时有三个;
当16<S<20时,-2<m<0中m只有一个值;
当S=16时,m=4或m=4-4![]() 这两个. 故当S=16时,相应的点P有且只有两个
这两个. 故当S=16时,相应的点P有且只有两个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为___________

-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形
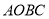 中,
中,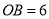 ,
,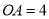 .分别以
.分别以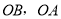 所在直线为
所在直线为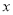 轴和
轴和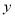 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系.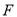 是边
是边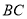 上一点,过点
上一点,过点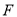 的反比例函数
的反比例函数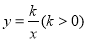 图象与
图象与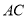 边交于点
边交于点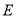 .
.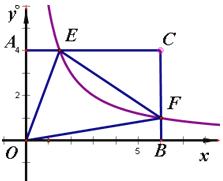
(1)请用k表示点E,F的坐标;
(2)若
 的面积为
的面积为 ,求反比例函数的解析式.
,求反比例函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据某网站调查,2014年网民们最关注的热点话题分别有:消费、教育、环保、反腐及其它五类,根据调查的部分相关数据,绘制的统计图表如下:
根据所给信息解答下列问题:
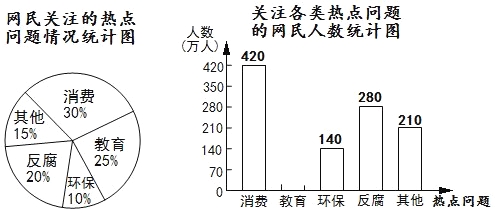
(1)请补全条形统计图并在图中标明相应数据;
(2)若菏泽市约有880万人口,请你估计最关注环保问题的人数为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
 解:∵EF∥AD (已知)
解:∵EF∥AD (已知)∴∠2= ( )
又∵∠1=∠2 (已知)∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=75°(已知)
∴∠AGD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
(1)当动点P与点B重合时,若点B的坐标是(2,1),求PA的长.
(2)当动点P在线段OB的延长线上时,若点A的纵坐标与点B的横坐标相等,求PA:PC的值.
(3)在(2)的条件下,已知AB=3,OB:BP=3:1,求四边形AOCP的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为( )
A.相离 B.相切 C.相交 D.无法确定
相关试题

