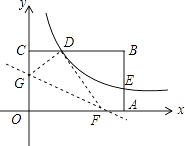
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y= ![]() (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,
(k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3, ![]() ).
). 
(1)求反比例函数的表达式和m的值;
(2)将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式.
参考答案:
【答案】
(1)解:∵反比例函数y= ![]() (k≠0)在第一象限内的图象经过点E(3,
(k≠0)在第一象限内的图象经过点E(3, ![]() ),
),
∴k=3× ![]() =2,
=2,
∴反比例函数的表达式为y= ![]() .
.
又∵点D(m,2)在反比例函数y= ![]() 的图象上,
的图象上,
∴2m=2,解得:m=1
(2)解:设OG=x,则CG=OC﹣OG=2﹣x,
∵点D(1,2),
∴CD=1.
在Rt△CDG中,∠DCG=90°,CG=2﹣x,CD=1,DG=OG=x,
∴CD2+CG2=DG2,即1+(2﹣x)2=x2,
解得:x= ![]() ,
,
∴点G(0, ![]() ).
).
过点F作FH⊥CB于点H,如图所示.
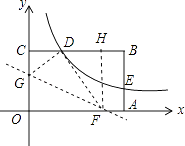
由折叠的特性可知:∠GDF=∠GOF=90°,OG=DG,OF=DF.
∵∠CGD+∠CDG=90°,∠CDG+∠HDF=90°,
∴∠CGD=∠HDF,
∵∠DCG=∠FHD=90°,
∴△GCD∽△DHF,
∴ ![]() =2,
=2,
∴DF=2GD= ![]() ,
,
∴点F的坐标为( ![]() ,0).
,0).
设折痕FG所在直线的函数关系式为y=ax+b,
∴有 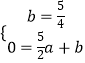 ,解得:
,解得:  .
.
∴折痕FG所在直线的函数关系式为y=﹣ ![]() x+
x+ ![]()
【解析】(1)由点E的坐标利用反比例函数图象上点的坐标特征即可求出k值,再由点B在反比例函数图象上,代入即可求出m值;(2)设OG=x,利用勾股定理即可得出关于x的一元二次方程,解方程即可求出x值,从而得出点G的坐标.再过点F作FH⊥CB于点H,由此可得出△GCD∽△DHF,根据相似三角形的性质即可求出线段DF的长度,从而得出点F的坐标,结合点G、F的坐标利用待定系数法即可求出结论.
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+5经过点B(3,9)和A(﹣6,m).
(1)求k,m的值;
(2)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B,C都在半径为r的圆上,直线AD⊥直线BC,垂足为D,直线BE⊥直线AC,垂足为E,直线AD与BE相交于点H.若BH=
 AC,则∠ABC所对的弧长等于(长度单位).
AC,则∠ABC所对的弧长等于(长度单位). -
科目: 来源: 题型:
查看答案和解析>>【题目】曲靖市某商场投入19200元资金购进甲、乙两种饮料共600箱,饮料的成本价和销售价如表所示:
类别/单价
成本价
销售价(元/箱)
甲
24
36
乙
36
52
(1)该商场购进甲、乙两种饮料各多少箱?
(2)全部售完600箱饮料,该商场共获得利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个布袋中装有只有颜色不同的a(a>12)个球,分别是2个白球,4个黑球,6个红球和b个黄球,从中任意摸出一个球,把摸出白球,黑球,红球的概率绘制成统计图(未绘制完整).请补全该统计图并求出
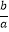 的值.
的值. 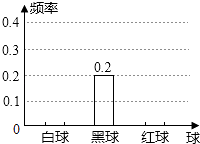
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E为正方形ABCD中AD边上的一个动点,AB=16,以BE为边画正方形BEFG,边EF与边CD交于点H.
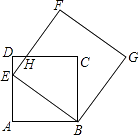
(1)当E为边AD的中点时,求DH的长;
(2)当tan∠ABE= 时,连接CF,求CF的长;
时,连接CF,求CF的长;
(3)连接CE,求△CEF面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=﹣
 x+3与x轴、y轴分别相交于点A、B,再将△A0B沿直钱CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
x+3与x轴、y轴分别相交于点A、B,再将△A0B沿直钱CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.(1)点A的坐标为 ;点B的坐标为 ;
(2)求OC的长度,并求出此时直线BC的表达式;
(3)直线BC上是否存在一点M,使得△ABM的面积与△ABO的面积相等?若存在,请直接写出点M的坐标;若不存在,请说明理由.

相关试题

