【题目】已知△ABC, ①如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+ ![]() ∠A;
∠A;
②如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°﹣∠A;
③如图3,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°﹣ ![]() ∠A.
∠A.
上述说法正确的个数是( )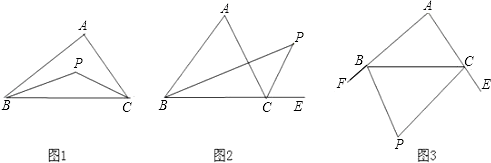
A.3个
B.2个
C.1个
D.0个
参考答案:
【答案】C
【解析】解:①若P点是∠ABC和∠ACB的角平分线的交点, 则∠PBC= ![]() ∠ABC,∠PCB=
∠ABC,∠PCB= ![]() ∠ACB
∠ACB
则∠PBC+∠PCB= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°﹣∠A)
(180°﹣∠A)
在△BCP中利用内角和定理得到:
∠P=180﹣(∠PBC+∠PCB)=180﹣ ![]() (180°﹣∠A)=90°+
(180°﹣∠A)=90°+ ![]() ∠A,
∠A,
故成立;
②当△ABC是等腰直角三角形,∠A=90°时,结论不成立;
③若P点是外角∠CBF和∠BCE的角平分线的交点,
则∠PBC= ![]() ∠FBC=
∠FBC= ![]() (180°﹣∠ABC)=90°﹣
(180°﹣∠ABC)=90°﹣ ![]() ∠ABC,
∠ABC,
∠BCP= ![]() ∠BCE=90°﹣
∠BCE=90°﹣ ![]() ∠ACB
∠ACB
∴∠PBC+∠BCP=180°﹣ ![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
又∵∠ABC+∠ACB=180°﹣∠A
∴∠PBC+∠BCP=90°+ ![]() ∠A,
∠A,
在△BCP中利用内角和定理得到:
∠P=180﹣(∠PBC+∠PCB)=180﹣ ![]() (180°+∠A)=90°﹣
(180°+∠A)=90°﹣ ![]() ∠A,
∠A,
故成立.
∴说法正确的个数是2个.
故选C.
【考点精析】本题主要考查了三角形的内角和外角和三角形的外角的相关知识点,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE , 若∠CAE=65°,∠E=70°,且AD⊥BC , 则∠BAC的度数为( )
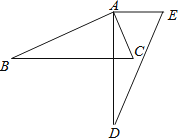
A.60°
B.85°
C.75°
D.90° -
科目: 来源: 题型:
查看答案和解析>>【题目】A城有某种农机30台,B城有该农机40台,现要将这些农机全部运往C,D两乡,调运任务承包给某运输公司.已知C乡需要农机34台,D乡需要农机36天,从A城往C,D两乡运送农机的费用分别为250元/台和200元/台,从B城往C,D两乡运送农机的费用分别为150元/台和240元/台.
(1)设A城运往C乡该农机x台,运送全部农机的总费用为W元,求W关于x的函数关系式,并写出自变量x的取值范围;
(2)现该运输公司要求运送全部农机的总费用不低于16460元,则有多少种不同的调运方案?将这些方案设计出来;
(3)现该运输公司决定对A城运往C乡的农机,从运输费中每台减免a元(a≤200)作为优惠,其它费用不变,如何调运,使总费用最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘轮船在同一航线上往返于甲、乙两地.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为(h),航行的路程为s(km),则s与的函数图象大致是( )
A.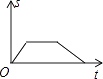
B.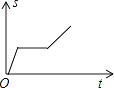
C.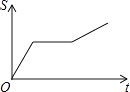
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中正确的是( )
A. (x+2)2=x2+2x+4 B. (-3-x)(3+x)=9-x2
C. (-3-x)(3+x)=-x2-9+6x D. (2x-3y)2=4x2+9y2-12xy
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中不能用平方差公式进行因式分解的是( )
A. 1-a4 B. -16a2+b2 C. -m4-n4 D. 9a2-b4
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升
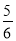 cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
相关试题

