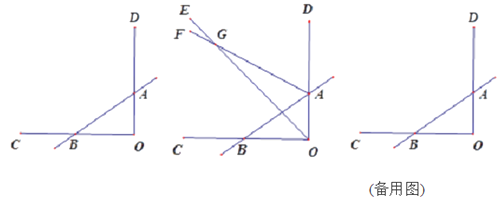
【题目】已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE与射线AF交于点G.
(1)若OE平分∠BOA,AF平分∠BAD,∠OBA=42°,则∠OGA= ;
(2)若∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD,∠OBA=42°,则∠OGA= ;
∠BAD,∠OBA=42°,则∠OGA= ;
(3)将(2)中的“∠OBA=42°”改为“∠OBA=![]() ”,其它条件不变,求∠OGA的度数.(用含
”,其它条件不变,求∠OGA的度数.(用含![]() 的代数式表示)
的代数式表示)
(4)若OE将∠BOA分成1︰2两部分,AF平分∠BAD,∠ABO=![]() (30°<
(30°<![]() <90°) ,求∠OGA的度数.(用含
<90°) ,求∠OGA的度数.(用含![]() 的代数式表示)
的代数式表示)
参考答案:
【答案】(1)∠OGA=21°;
(2)∠OGA=14°;
(3)∠OGA=![]() ;
;
(4)∠OGA的度数为![]() 或
或![]()
【解析】试题分析:(1)根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,根据三角形外角性质求出即可;(2)根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,根据三角形外角性质求出即可;(3)根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,根据三角形外角性质求出即可;(4)讨论:当∠EOD:∠COE=1:2时,利用∠BAD=∠ABO+∠BOA=β+90°,∠FAD=∠EOD+∠OGA得到2×30°+2∠OGA=β+90°,则∠OGA=![]() β+15°;当∠EOD:∠COE=2:1时,则∠EOD=60°,同理得∠OGA=
β+15°;当∠EOD:∠COE=2:1时,则∠EOD=60°,同理得∠OGA=![]() β-15°.
β-15°.
试题解析:(1)∵∠BOA=90°,∠OBA=42°,
∴∠BAD=∠BOA+∠ABO=132°,
∵AF平分∠BAD,OE平分∠BOA,∠BOA=90°,
∴∠GAD=![]() ∠BAD=66°,∠EOA=
∠BAD=66°,∠EOA=![]() ∠BOA=45°,
∠BOA=45°,
∴∠OGA=∠GAD∠EOA=66°45°=21°;
故答案为21°;
(2)∵∠BOA=90°,∠OBA=42°,
∴∠BAD=∠BOA+∠ABO=132°,
∵∠BOA=90°,∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD
∠BAD
∴∠GAD=44°,∠EOA=30°,
∴∠OGA=∠GAD∠EOA=44°30°=14°;
故答案为14°;
(3)∵∠BOA=90°,∠OBA=α,
∴∠BAD=∠BOA+∠ABO=90°+α,
∵∠BOA=90°,∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD
∠BAD
∴∠GAD=30°+![]() α,∠EOA=30°,
α,∠EOA=30°,
∴∠OGA=∠GAD∠EOA=![]() α,
α,
故答案为:![]() α;
α;
(4)当∠EOD:∠COE=1:2时,
则∠EOD=30°,
∵∠BAD=∠ABO+∠BOA=α+90°,
∵AF平分∠BAD,
∴∠FAD=![]() ∠BAD,
∠BAD,
∵∠FAD=∠EOD+∠OGA,
∴2×30°+2∠OGA=α+90°,
∴∠OGA=![]() α+15°;
α+15°;
当∠EOD:∠COE=2:1时,则∠EOD=60°,
同理得到∠OGA=![]() α15°,
α15°,
即∠OGA的度数为![]() α+15°或
α+15°或![]() α15°.
α15°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算-7-1的结果为( )
A. 7 B. -6 C. -8 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程ax2﹣4x﹣1=0是一元二次方程,则a满足的条件是( )
A. a>0 B. a≠0 C. a<0 D. a≠4
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算m2+2m2的结果是( )
A. 2m4 B. 3m2 C. 3m4 D. 2m2
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图(1),若分别以△ABC的三边AC、BC、AB为边向三角形外侧作正方形ACDE、BCFG和ABMN,则称这三个正方形为△ABC的外展三叶正方形,其中任意两个正方形为△ABC的外展
双叶正方形.
(1)作△ABC的外展双叶正方形ACDE和BCFG,记△ABC,△DCF的面积分别为S1和S2.
①如图(2),当∠ACB=90°时,求证:S1=S2;
②如图(3),当∠ACB≠90°时,S1与S2是否仍然相等,请说明理由.
(2)已知△ABC中,AC=3,BC=4,作其外展三叶正方形,记△DCF、△AEN、△BGM的面积和为S,请利用图(1)探究:当∠ACB的度数发生变化时,S的值是否发生变化?若不变,求出S的值;若变化,求出S的最大值.

-
科目: 来源: 题型:
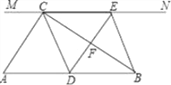
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明编了一个程序:输入任何一个有理数时,显示屏上的结果总等于输入的有理数的平方减去2得到的差。若他第一次输入-3,然后再将所得的结果输入,这时显示屏出现的结果是____________.
相关试题

