【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.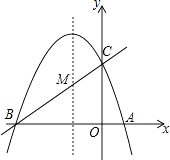
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
参考答案:
【答案】
(1)
解:依题意得:  ,
,
解之得:  ,
,
∴抛物线解析式为y=﹣x2﹣2x+3
∵对称轴为x=﹣1,且抛物线经过A(1,0),
∴把B(﹣3,0)、C(0,3)分别代入直线y=mx+n,
得 ![]() ,
,
解之得: ![]() ,
,
∴直线y=mx+n的解析式为y=x+3
(2)
解:设直线BC与对称轴x=﹣1的交点为M,则此时MA+MC的值最小.
把x=﹣1代入直线y=x+3得,y=2,
∴M(﹣1,2),
即当点M到点A的距离与到点C的距离之和最小时M的坐标为(﹣1,2)
(3)
解:设P(﹣1,t),
又∵B(﹣3,0),C(0,3),
∴BC2=18,PB2=(﹣1+3)2+t2=4+t2,PC2=(﹣1)2+(t﹣3)2=t2﹣6t+10,
①若点B为直角顶点,则BC2+PB2=PC2即:18+4+t2=t2﹣6t+10解之得:t=﹣2;
②若点C为直角顶点,则BC2+PC2=PB2即:18+t2﹣6t+10=4+t2解之得:t=4,
③若点P为直角顶点,则PB2+PC2=BC2即:4+t2+t2﹣6t+10=18解之得:t1= ![]() ,t2=
,t2= ![]() ;
;
综上所述P的坐标为(﹣1,﹣2)或(﹣1,4)或(﹣1, ![]() ) 或(﹣1,
) 或(﹣1, ![]() ).
).
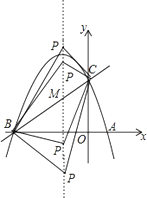
【解析】(1)先把点A,C的坐标分别代入抛物线解析式得到a和b,c的关系式,再根据抛物线的对称轴方程可得a和b的关系,再联立得到方程组,解方程组,求出a,b,c的值即可得到抛物线解析式;把B、C两点的坐标代入直线y=mx+n,解方程组求出m和n的值即可得到直线解析式;(2)设直线BC与对称轴x=﹣1的交点为M,则此时MA+MC的值最小.把x=﹣1代入直线y=x+3得y的值,即可求出点M坐标;(3)设P(﹣1,t),又因为B(﹣3,0),C(0,3),所以可得BC2=18,PB2=(﹣1+3)2+t2=4+t2 , PC2=(﹣1)2+(t﹣3)2=t2﹣6t+10,再分三种情况分别讨论求出符合题意t值即可求出点P的坐标.
-
科目: 来源: 题型:
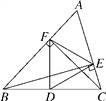
查看答案和解析>>【题目】如图,在△ABC中,∠A=60°,BE⊥AC,垂足为E,CF⊥AB,垂足为F,点D是BC的中点.
(1)求证:DE=DF;
(2)试猜想△DEF是不是等边三角形?如果是,请加以证明;如果不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新学期开学,某体育用品商店开展促销活动,有两种优惠方案.
方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.
方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:

会员卡只限本人使用.
(1)求该商店销售的乒乓球拍每副的标价.
(2)如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a盒,请回答下列问题:
①如果方案一与方案二所付钱数一样多,求a的值;
②直接写出一个恰当的a值,使方案一比方案二优惠;
③直接写出一个恰当的a值,使方案二比方案一优惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
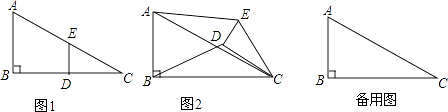
(1)问题发现
①当α=0°时, =;②当α=180°时,
=;②当α=180°时,  = .
= .
(2)拓展探究
试判断:当0°≤α<360°时, 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长. -
科目: 来源: 题型:
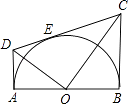
查看答案和解析>>【题目】如图,AB为半圆O在直径,AD,BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD,OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:EC,⑤OD2=DECD,正确的有( )
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】标准的篮球场长28m,宽15m.在某场篮球比赛中,红队甲、乙两名运动员分别在A,B处,位置如图①所示,已知点B到中线EF的距离为6m,点C到中线EF的距离为8m,运动员甲在A处抢到篮球后,迅速将球抛向C处,球的平均运行速度是
 m/s,运动员乙在B处看到后同时快跑到C处并恰好接住了球(点A,B,C在同一直线上).图②中l1,l2分别表示球、运动员乙离A处的距离y(m)与从A处抛球后的时间x(s)的关系图象.
m/s,运动员乙在B处看到后同时快跑到C处并恰好接住了球(点A,B,C在同一直线上).图②中l1,l2分别表示球、运动员乙离A处的距离y(m)与从A处抛球后的时间x(s)的关系图象.(1)直接写出a,b,c的值;
(2)求运动员乙由B处跑向C处的过程中y(m)与x(s)的函数解析式l2;
(3)运动员要接住球,一般在球距离自己还有2m远时要做接球准备,求运动员乙准备接此球的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两地相距450千米,两地之间有一个加油站O,且AO=270千米,一辆轿车从A地出发,以每小时90千米的速度开往B地,一辆客车从B地出发,以每小时60千米的速度开往A地,两车同时出发,设出发时间为t小时.
(1)经过几小时两车相遇?
(2)当出发2小时时,轿车和客车分别距离加油站O多远?
(3)经过几小时,两车相距50千米?

相关试题

