【题目】如图:在长方形ABCD中, AB=CD=4cm,BC=3cm,动点P从点A出发,先以1cm/s的速度沿A→B,然后以2cm/s的速度沿B→C运动,到C点停止运动,设点P运动的时间为t秒,是否存在这样的t,使得△BPD的面积S>3cm2?如果能,请求出t的取值范围;如果不能,请说明理由.

参考答案:
【答案】存在这样的t,使得△BPD的面积满足条件,此时0≤t<2;![]() <t≤5.5.
<t≤5.5.
【解析】
试题分两段考虑:①点P在AB上,②点P在BC上,分别用含t的式子表示出△BPD的面积,再由S>3cm2建立不等式,解出t的取值范围值即可.
试题解析:①当点P在AB上时,假设存在△BPD的面积满足条件,即运动时间为t秒,则
S△BPD=![]() (4-t)×3=
(4-t)×3=![]() (4-t)>3
(4-t)>3
解得t<2,
又因为P在AB上运动,0≤t≤4,
所以0≤t<2;
②当点P在BC上时,假设存在△BPD的面积满足条件,即运动时间为t秒,则
S△BPD=![]() (4-t)×2×4=4t-16>3
(4-t)×2×4=4t-16>3
解得t>![]() ,
,
又因为P在BC上运动,4<t≤5.5,
所以![]() <t≤5.5;
<t≤5.5;
综上所知,存在这样的t,使得△BPD的面积满足条件,此时0≤t<2;![]() <t≤5.5.
<t≤5.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图1,写出点D到△ABC三个顶点A,B,C的距离的关系(直接写出结论);
(2)如图1,点E,F分别是AB,AC上的点,且BE=AF,求证:△DEF是等腰直角三角形;
(3)若点E,F分别是AB,CA的延长线上的点,仍有BE=AF,其他条件不变,请判断△DEF的形状?(直接写结论).


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.

(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与双曲线的另一交点为D点,求△ODB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】用两种方法证明“四边形的外角和等于360°”.
如图,∠DAE、∠ABF、∠BCG、∠CDH是四边形ABCD的四个外角.
求证:∠DAE+∠ABF+∠BCG+∠CDH=360°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AB=5cm,AC⊥AB,BD⊥AB,AC=BD=4cm,点P在线段AB上以1cm/s的速度由A向B运动,同时,点Q在线段BD上由点B向点D运动,它们运动时间为t(s).
(1)若点Q的运动速度与点P速度相等,当t=1,△ACP与△BPQ是否全等?请说明理由,并推导出此时线段PC和线段PQ的位置关系;
(2)如图2,将图1中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=α°”,其他条件不变,设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x,t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.以OC为一边作等边三角形OCD,连接AC、AD.当△AOD是等腰三角形时,求α的角度为______

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
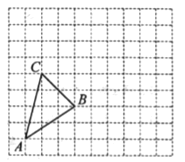
(1)画出△ABC先向右平移5个单位长度,再向上平移2个单位长度所得的△A1B1C1;
(2)画出△ABC的中线AD;
(3)画出△ABC的高CE所在直线,标出垂足E:
(4)在(1)的条件下,线段AA1和CC1的关系是
相关试题

