【题目】如图,点O是直线AB、CD的交点,∠AOE=∠COF=![]() ,
,
①如果∠EOF=![]() ,求∠AOD的度数;
,求∠AOD的度数;
②如果∠EOF=![]() ,求∠AOD的度数.
,求∠AOD的度数.

参考答案:
【答案】(1)148°;(2)180°-x°.
【解析】
(1)根据∠AOE=∠COF=90°,可知∠COF=∠BOE=90°,进而求出∠BOD的度数,根据补角的定义可以求出∠AOD的度数;
(2)解法和(1)相同,只是∠EOF=x°,还是根据补角的定义可以求出∠AOD的度数.
解:(1)∵∠AOE=∠COF=90°,
∴∠COF=∠BOE=90°,
∵∠EOF=32°,
∴∠BOD=∠EOF=32°,
∴∠AOD=180°-∠BOD=148°;
(2)∵∠EOF=x°,
∴∠BOD=x°,
∴∠AOD=180°-∠BOD=180°-x°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有【 】个.

A.2 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点C在直线AB上,AC=8cm,BC=6cm,点M、N分别是AC、BC的中点,求线段MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上,A、B两地相距300千米.甲乙两车分别从A、B两地同时出发,已知甲车速度为100千米/小时,乙车速度为60千米/小时.经过一段时间后,两车相距100千米,求两车的行驶时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分)已知:如图,△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE;垂足为E.
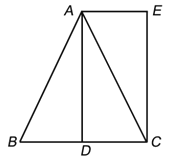
(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别为BE,BC,CE的中点.
(1)试说明四边形EGFH是平行四边形;
(2)在(1)的条件下,若EF⊥BC,且EF=
 BC,试说明平行四边形EGFH是正方形.
BC,试说明平行四边形EGFH是正方形.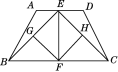
相关试题

