【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
参考答案:
【答案】3或6
【解析】试题分析:
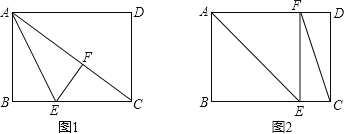
由题意可知有两种情况,见图1与图2;
图1:当点F在对角线AC上时,∠EFC=90°,
∵∠AFE=∠B=90°,∠EFC=90°,
∴点A、F、C共线,
∵矩形ABCD的边AD=8,
∴BC=AD=8,
在Rt△ABC中,AC=![]() =10,
=10,
设BE=x,则CE=BC﹣BE=8﹣x,
由翻折的性质得,AF=AB=6,EF=BE=x,
∴CF=AC﹣AF=10﹣6=4,
在Rt△CEF中,EF2+CF2=CE2,
即x2+42=(8﹣x)2,
解得x=3,
即BE=3;
图2:当点F落在AD边上时,∠CEF=90°,
由翻折的性质得,∠AEB=∠AEF=![]() ×90°=45°,
×90°=45°,
∴四边形ABEF是正方形,
∴BE=AB=6,
综上所述,BE的长为3或6.
故答案为:3或6.
-
科目: 来源: 题型:
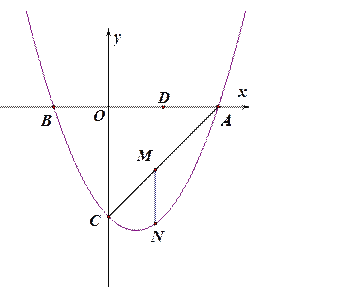
查看答案和解析>>【题目】如图,抛物线
 与y轴交于点C,与x轴交于点A和点B.若N点是AC所在直线下方该抛物线上的一个动点,过点N作MN平行于
与y轴交于点C,与x轴交于点A和点B.若N点是AC所在直线下方该抛物线上的一个动点,过点N作MN平行于 轴,交AC于点M.
轴,交AC于点M.(1) 求直线AC的解析式;
(2)当点N运动至抛物线的顶点时,求此时MN的长;
(3)设点N的横坐标为t,MN的长度为l;
①求l与t之间的函数关系式,并写出t的取值范围;
②l是否存在最值,有如有写出最值;
(4)点D是点B关于
 轴的对称点.抛物线上是否有点N,使△ODM是等腰三角形?
轴的对称点.抛物线上是否有点N,使△ODM是等腰三角形?若存在,请求出此时△CAN的面积;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】商店某天销售了11件衬衫,其领口尺寸统计如下表:
领口尺寸(单位:cm)
38
39
40
41
42
件数
1
4
3
1
2
则这11件衬衫领口尺寸的众数是__________cm,中位数是__________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“对顶角相等”的题设是_______________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,C、D是半径OA、OB的中点且OA⊥CE、OB⊥DE,求证:


-
科目: 来源: 题型:
查看答案和解析>>【题目】点(1,﹣3)关于y轴对称点的坐标是( )
A. (﹣1,﹣3) B. (﹣3,1) C. (﹣1,3) D. (1,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式2﹣3xy﹣52xy2的最高次项系数和次数分别是( )
A.﹣5,5
B.﹣5,3
C.52 , 3
D.﹣52 , 3
相关试题

