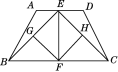
【题目】如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别为BE,BC,CE的中点.
(1)试说明四边形EGFH是平行四边形;
(2)在(1)的条件下,若EF⊥BC,且EF=![]() BC,试说明平行四边形EGFH是正方形.
BC,试说明平行四边形EGFH是正方形.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
通过中位线定理得出GF∥EH且GF=EH,所以四边形EGFH是平行四边形;
当添加了条件EF⊥BC,且EF=![]() BC后,通过对角线相等且互相垂直平分(EF⊥GH,且EF=GH)就可证明是正方形.
BC后,通过对角线相等且互相垂直平分(EF⊥GH,且EF=GH)就可证明是正方形.
解:(1)在△BEC中,
∵G,F分别是BE,BC的中点,
∴GF∥EC(即GF∥EH)且GF=![]() EC.
EC.
∵H为EC的中点,∴EH=![]() EC,
EC,
∴GF=EH.
∴四边形EGFH是平行四边形.
(2)连接GH.∵G,H分别是BE,CE的中点,
∴GH∥BC且GH=![]() BC,
BC,
又∵EF⊥BC且EF=![]() BC,
BC,
∴EF⊥GH且EF=GH.
∴平行四边形EGFH是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线AB、CD的交点,∠AOE=∠COF=
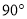 ,
,①如果∠EOF=
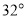 ,求∠AOD的度数;
,求∠AOD的度数;②如果∠EOF=
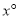 ,求∠AOD的度数.
,求∠AOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上,A、B两地相距300千米.甲乙两车分别从A、B两地同时出发,已知甲车速度为100千米/小时,乙车速度为60千米/小时.经过一段时间后,两车相距100千米,求两车的行驶时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分)已知:如图,△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE;垂足为E.
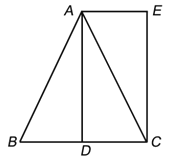
(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E是BC边上一点,且BE:EC=2:1,AE与BD交于点F,则△AFD与四边形DFEC的面积之比是 .
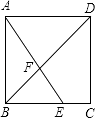
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(π﹣3.14)0+|
 ﹣1|﹣(
﹣1|﹣( 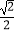 )﹣1﹣2sin45°+(﹣1)2016 .
)﹣1﹣2sin45°+(﹣1)2016 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某人去水果批发市场采购猕猴桃,他看中了A、B两家猕猴桃.这两家猕猴桃品质一样,零售价都为6元/千克,批发价各不相同,
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如下表:
数量范围
(千克)
0~500
500以上~1500
1500以上~2500
2500以上
价格(元)
零售价的95%
零售价的85%
零售价的75%
零售价的70%
(1)如果他批发600千克猕猴桃,则他在A 、B两家批发分别需要多少元?
(2)如果他批发x千克猕猴桃(1500<x<2000),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发1800千克猕猴桃,你能帮助他选择在哪家批发更优惠吗?请说明理由.
相关试题

