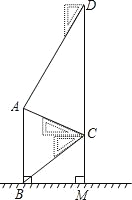
【题目】如图，某中学在教学楼前新建了一座雕塑AB．为了测量雕塑的高度，小明在二楼找到一点C，利用三角尺测得雕塑顶端点A的仰角为30°，底部点B的俯角为45°，小华在五楼找到一点D，利用三角尺测得点A的俯角为60°．若CD为9.6m，则雕塑AB的高度为多少？（结果精确到0.1m，参考数据：≈1.73）．

参考答案：

【答案】雕塑AB的高度约为6.6米．

【解析】

试题分析：首先过点C作CE⊥AB于E，然后利用三角函数的性质，求得CD，AC的长，然后在Rt△ACE中，求得AE的长，继而求得CE的长，又在Rt△BCE中，求得BE的长，继而求得答案．

试题解析：过点C作CE⊥AB于E．

∵∠ADC=90°-60°=30°，∠ACD=90°-30°=60°，

∴∠CAD=90°．

∵CD=9.6，

∴AC=CD=4.8．

在Rt△ACE中，∵∠AEC=90°，∠ACE=30°，

∴AE=AC=2.4，

CE=ACcos∠ACE=4.8cos30°=．

在Rt△BCE中，∵∠BCE=45°，

∴BE=CE=，

∴AB=AE+BE=2.4+≈6.6（米）．

答：雕塑AB的高度约为6.6米．

关闭