【题目】如图,一辆动车从A地开往B地,一辆高铁从B地开往A地.两车同时出发,设动车离A地的距离为y1(km),高铁离A地的距离为y2(km),动车行驶时间为t(h),变量y1、y2之间的关系图象如图所示:
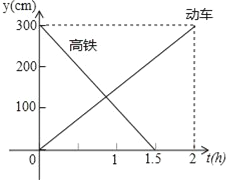
(1)根据图象,求高铁和动车的速度;
(2)动车出发多少小时与高铁相遇;
(3)两车出发经过多长时间相距50km.
参考答案:
【答案】(1)高铁的速度为200km/h,动车的速度为150km/h;(2)动车出发![]() 小时与高铁相遇;(3)当x=1或
小时与高铁相遇;(3)当x=1或![]() 时两车相距50km.
时两车相距50km.
【解析】试题分析:(1)由题意结合图,即可得出速度;
(2)先分别求出解析式,然后联立组成方程组,解方程组即可得;
(3)将(2)中得到的两个解析式互相减即可得.
试题解析:(1)高铁的速度为:300÷1.5=200(km/h),
动车的速度为:300÷2=150(km/h).
(2)设高铁的函数解析式为:y1=kx+b,
把(0,300),(1.5,0)代入y=kx+b得: ![]() ,
,
解得: ![]() ,则y1=﹣200x+300,
,则y1=﹣200x+300,
动车的函数解析式为:y2=150x,
当动车与高铁相遇时,即﹣200x+300=150x
解得:x=![]() .
.
答:动车出发![]() 小时与高铁相遇;
小时与高铁相遇;
(3)当y1=y2时,两车相遇,解得x=![]() ,
,
①0≤x≤![]() 时,y1﹣y2=﹣200x+300﹣150x=50,得:x=
时,y1﹣y2=﹣200x+300﹣150x=50,得:x=![]() ,
,
②![]() <x≤1.5时,y2﹣y1=150x﹣(﹣200x+300)=50,得:x=1,
<x≤1.5时,y2﹣y1=150x﹣(﹣200x+300)=50,得:x=1,
综上所述:当x=1或![]() 时两车相距50km.
时两车相距50km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:3x(x-2)=4-2x. (2)用配方法解方程:
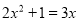
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣9)﹣(﹣3)的结果是( )
A.﹣12
B.﹣6
C.+6
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是外角和的3倍,则这个多边形是( )
A.六边形
B.七边形
C.八边形
D.九边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程
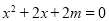 有两个不相等的实数根.
有两个不相等的实数根.(1)求m的取值范围;
(2)若
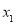 ,
,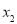 是一元二次方程
是一元二次方程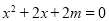 的两个根,且
的两个根,且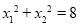 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为促进朗诵艺术的普及、发展,挖掘播音主持人才,某校初二年级举办朗诵大赛,凡凡同学根据比赛中九位评委所给的某位参赛选手的分数,制作了一个表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
中位数
众数
平均数
方差
9.2
9.3
9.1
0.3
A.中位数
B.众数
C.平均数
D.方差 -
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一道题:“先化简,再求值:(3x2﹣2x+4)﹣2(x2﹣x)﹣x2,其中x=100”甲同学做题时把x=100错抄成了x=10,乙同学没抄错,但他们做出来的结果却一样,你能说明这是为什么吗?并求出这个结果.
相关试题

