【题目】(1)解方程:3x(x-2)=4-2x. (2)用配方法解方程: ![]()
参考答案:
【答案】(1)x1=2,x2=![]() ;(2)x1=1,x2=
;(2)x1=1,x2=![]()
【解析】(1)把右边的项移到左边,用提公因式法因式分解求出方程的根;(2)首先把方程的二次项系数变成1,然后方程两边同时加上一次项系数的一半,则方程的左边就是完全平方式,右边是常数的形式,再利用直接开平方的方法即可求解.
解:(1)3x(x–2)– 2(2– x)=0,
3x(x–2)+ 2(x–2)=0,
(x–2)(3x+2)=0,
∴x–2=0,3x+2=0,
解得x1=2,x2=![]() .
.
(2)移项,得2x2–3x= –1,
二次项系数化为1,x2–![]() x=
x=![]() ,
,
配方,得x2–![]() x+
x+![]() =
=![]() +
+![]() ,
,
开方,得(x![]() )2=
)2=![]() ,
,
由此可得x![]() ,
,
解得,x1=1,x2=![]() .
.
“点睛”(1)考查的是用因式分解法解方程,根据题目的结构特点,用提公因式法因式分解求出方程的根.(2)考查了配方法解方程.配方法的一般步骤:①把常数项移到等号的右边;②把二次项的系数化为1;③等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在公式s=s0+vt中,已知s=100,s0=25,v=10,则t= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,m+2的算术平方根是2,2m+n的立方根是3,则m+n=_____.
-
科目: 来源: 题型:
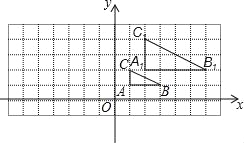
查看答案和解析>>【题目】如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1.
(1)△A1B1C1与△ABC的位似比是 ;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)设点P(a,b)为△ABC内一点,则依上述两次变换后,点P在△A2B2C2内的对应点P2的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣9)﹣(﹣3)的结果是( )
A.﹣12
B.﹣6
C.+6
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是外角和的3倍,则这个多边形是( )
A.六边形
B.七边形
C.八边形
D.九边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一辆动车从A地开往B地,一辆高铁从B地开往A地.两车同时出发,设动车离A地的距离为y1(km),高铁离A地的距离为y2(km),动车行驶时间为t(h),变量y1、y2之间的关系图象如图所示:
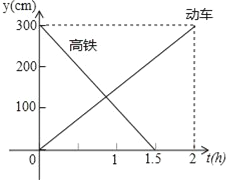
(1)根据图象,求高铁和动车的速度;
(2)动车出发多少小时与高铁相遇;
(3)两车出发经过多长时间相距50km.
相关试题

