【题目】如图,E是BC的中点,BE=![]() ,AD=
,AD=![]() .
.
(1)求线段BC、AB的长;
(2)求线段AC的长;
(3)求线段DE的长.
![]()
参考答案:
【答案】(1)BC=4cm,AB =6cm;(2)AC=10cm;(3)DE=6cm
【解析】
(1)根据线段中点的性质,可得BC的长,进而得出AB的长;(2)根据线段的和差,可得AC的长;(3)根据AB=AD+DB,再利用![]() DB+DB=6,可得DB的长,再根据线段的和差,可得答案.
DB+DB=6,可得DB的长,再根据线段的和差,可得答案.
(1)由E是BC的中点,
BC=2BE=2×2=4cm,
由BE=![]() =2cm,得
=2cm,得
AB=3×2=6cm;
![]()
(2)由线段的和差,得
AC=AB+BC=4+6=10cm
(3)AB=AD+DB,
即![]() DB+DB=6cm,
DB+DB=6cm,
解得DB=4cm
由线段的和差,得
DE=DB+BE=4+2=6cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=﹣kx+k﹣3与直线y=kx在同一坐标系中的大致图象可能是( )
A.
 B.
B.  C.
C. 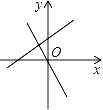 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC,AD=3,DF=1,四边形DBEC面积是_____

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=ax+b与双曲线y=
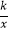 (x>0)在第一象限内交于A(x1 , y1),B(x2 , y2)两点,与x轴交于点C(x0 , 0)
(x>0)在第一象限内交于A(x1 , y1),B(x2 , y2)两点,与x轴交于点C(x0 , 0)
(1)若A(2,2)、B(4,n) ①求直线和双曲线解析式
②直接写出S△AOB=
(2)直接写出x1、x2、x0之间的数量关系.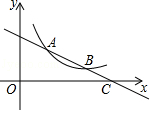
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.

(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, .求BE的长.
.求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)试判断四边形AEBO的形状,并说明你的理由;
(2)求证:EO=DC.

相关试题

