【题目】如图,△ABC的两条中线AM、BN相交于点O,已知△ABC的面积为14,△BOM的面积为3,求四边形MCNO的面积. 
参考答案:
【答案】解:∵△ABC的两条中线AM、BN相交于点O, ∴△BCN的面积=△ABC的面积的一半,
又∵△ABC的面积为14,
∴△BCN的面积=7,
又∵△BOM的面积为3,
∴四边形MCNO的面积=7﹣3=4.
【解析】先根据三角形的中线将三角形的面积分成相等的两部分,求得△BCN的面积,再根据△BOM的面积为3,求得四边形MCNO的面积.
【考点精析】通过灵活运用三角形的“三线”和三角形的面积,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内;三角形的面积=1/2×底×高即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
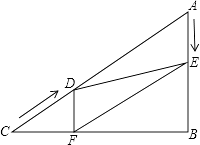
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由. -
科目: 来源: 题型:
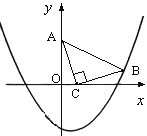
查看答案和解析>>【题目】如图,在直角坐标系中,已知点A(0, 3)、点C(1, 0),等腰Rt△ACB的顶点B在抛物线
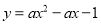 上.
上.(1)求点B的坐标及抛物线的解析式;
(2)在抛物线上是否存在点P(点B除外),使△ACP是以AC为直角边的Rt△?若存在,求出所有点P的坐标;若不存在,请说明理由.
(3)在抛物线上是否存在点Q(点B除外),使△ACQ是以AC为直角边的等腰Rt△?若存在直接写出所有点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是( )
A.菱形
B.对角线相互垂直的四边形
C.正方形
D.对角线相等的四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x2+x﹣6=0的两个根是a,b,则ab的值为( )
A.1
B.﹣1
C.6
D.﹣6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠B+∠C+∠D+∠E﹣∠A等于( )
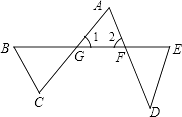
A.360°
B.300°
C.180°
D.240° -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣1)2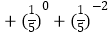
(2)[(﹣3a)2+3ab2c]2ab2
(3)(﹣ )100×3101
)100×3101
(4)(2a+b)(b﹣2a)﹣(a﹣3b)2 .
相关试题

