【题目】若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是( )
A.菱形
B.对角线相互垂直的四边形
C.正方形
D.对角线相等的四边形
参考答案:
【答案】B
【解析】解:已知:如右图,四边形EFGH是矩形,且E、F、G、H分别是AB、BC、CD、AD的中点,求证:四边形ABCD是对角线垂直的四边形. 证明:由于E、F、G、H分别是AB、BC、CD、AD的中点,
根据三角形中位线定理得:EH∥FG∥BD,EF∥AC∥HG;
∵四边形EFGH是矩形,即EF⊥FG,
∴AC⊥BD;故选B.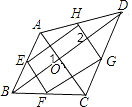
此题要根据矩形的性质和三角形中位线定理求解;首先根据三角形中位线定理知:所得四边形的对边都平行且相等,那么其必为平行四边形,若所得四边形是矩形,那么邻边互相垂直,故原四边形的对角线必互相垂直,由此得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】菏泽市大力推功新旧动能转换,产业转型升级迈出新步伐.建立了新旧动能转换项目,筛选论证项目325个,计划总投资3137亿元,3137亿用科学记数法表示为( )
A. 0.3137×1012B. 3.137×1012
C. 3.137×1011D. 3137×108
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
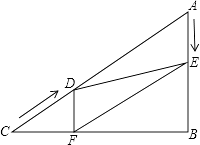
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由. -
科目: 来源: 题型:
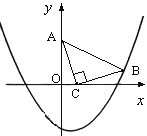
查看答案和解析>>【题目】如图,在直角坐标系中,已知点A(0, 3)、点C(1, 0),等腰Rt△ACB的顶点B在抛物线
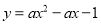 上.
上.(1)求点B的坐标及抛物线的解析式;
(2)在抛物线上是否存在点P(点B除外),使△ACP是以AC为直角边的Rt△?若存在,求出所有点P的坐标;若不存在,请说明理由.
(3)在抛物线上是否存在点Q(点B除外),使△ACQ是以AC为直角边的等腰Rt△?若存在直接写出所有点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的两条中线AM、BN相交于点O,已知△ABC的面积为14,△BOM的面积为3,求四边形MCNO的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x2+x﹣6=0的两个根是a,b,则ab的值为( )
A.1
B.﹣1
C.6
D.﹣6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠B+∠C+∠D+∠E﹣∠A等于( )
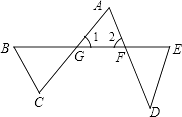
A.360°
B.300°
C.180°
D.240°
相关试题

