【题目】如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD是BC边上的高.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( ).
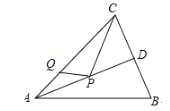
A.6B.8C.9.6D.12
参考答案:
【答案】C
【解析】
由“PC+PQ的最小值”可知本题考查的是两点之间垂线段最短的知识点,根据等腰三角形三线合一定理,可以找到PQ的对称点,从而找到点C到AB的垂线段交AD于点P,从而求出最小值
因为AB=AC,AD是BC的高,所以AD是∠BAC的角平分线,以AD为对称轴,作Q的对称点E,连接CE与AD交于点P,如图所示:
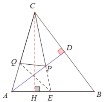
∵AD是∠BAC的角平分线
∴QP=PE
∴PC+PQ=PC+PE=EC
要使PC+PQ最小,即EC最小,所以CE是△ABC底边AB上的高的时候,CE最小
由三角形面积公式得: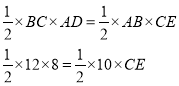 解得,CE=9.6,∴PC+PQ的最小值是9.6,答案选C
解得,CE=9.6,∴PC+PQ的最小值是9.6,答案选C
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C、D为圆心,大于
 CD的长为半径画弧,两弧在∠AOB内部交于点E,作射线OE,连接CD,以下说法错误的是( )
CD的长为半径画弧,两弧在∠AOB内部交于点E,作射线OE,连接CD,以下说法错误的是( )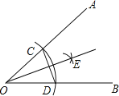
A.△OCD是等腰三角形B.CD垂直平分OE
C.点E到OA、OB的距离相等D.证明射线OE是角平分线的依据是SSS
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
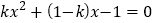 ,下列说法正确的是( )
,下列说法正确的是( )A. 当k=0时,方程没有实数根 B. 当k=1时,方程有一个实数根
C. 当k=-1时,方程有两个相等的实数根 D. 当k≠0时,方程总有两个不相等的实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,BC=3cm,CD⊥AB,垂足为点D.在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=7cm,则AE长为( ) .
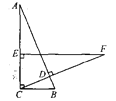
A.1cmB.2 cmC.3cmD.4cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,則四辺形ABFD的周长为( )

A. 16cmB. 18cmC. 20cmD. 22cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心都在原点,且各边也都与x轴或y轴平行,从内向外,它们的边长依次为2,4,6,8,…顶点依次用A1、A2、A3、A4表示,则顶点A2020的坐标为_____.
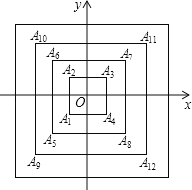
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
相关试题

