【题目】如图,直线y1=2x-2的图像与y轴交于点A,直线y2=-2x+6的图像与y轴交于点B,两者相交于点C.
(1)方程组![]() 的解是______;
的解是______;
(2)当y1>0与y2>0同时成立时,x的取值范围为_____;
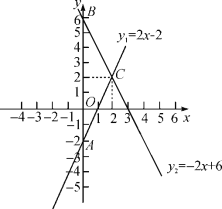
(3)求△ABC的面积;
(4)在直线y1=2x-2的图像上存在异于点C的另一点P,使得△ABC与△ABP的面积相等,请求出点P的坐标.
参考答案:
【答案】(1) ![]() ;(2) 1<x<3;(3)8;(4) P(-2,-6)
;(2) 1<x<3;(3)8;(4) P(-2,-6)
【解析】
(1)根据图像可知,两条直线的交点即为方程组的解;(2)找出两条直线的图像在x轴上方的公共部分的x的取值范围即可;(3)令x=0,求出y1与y2的值,即可得A、B两点的坐标,进而可得AB的长度,根据C点坐标为(2,2),可得△ABC的高,即可求出面积;(4)令P(x0,2x0-2),根据三角形面积公式可得x0=±2,由点P异于点C可得x0=-2,代入y1=2x-2即可的P点坐标.
(1)由图像可知直线y1=2x-2的图像与直线y2=-2x+6的交点坐标为(2,2)
∴方程组![]() 的解集为
的解集为![]() ,
,
(2)根据图像可知:当y1>0与y2>0同时成立时,x的取值范围为1<x<3.
(3)∵令x=0,则y1=-2,y2=6,
∴A(0,-2),B(0,6).
∴AB=8.
∴S△ABC=![]() ×8×2=8.
×8×2=8.
(4)令P(x0,2x0-2),则S△ABP=![]() ×8×|x0|=8,
×8×|x0|=8,
∴x0=±2.
∵点P异于点C,
∴x0=-2,2x0-2=-6.
∴P(-2,-6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
A型
B型
进价(元/盏)
40
65
售价(元/盏)
60
100
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
(3)若该商场预计用不少于2500元且不多于2600元的资金购进这批台灯,为了打开B种台灯的销路,商场决定每售出一盏B种台灯,返还顾客现金a元(10<a<20),问该商场该如何进货,才能获得最大的利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H,得到的四边形EFGH叫中点四边形.
(1)求证:四边形EFGH是平行四边形;
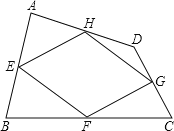
(2)如图,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空:
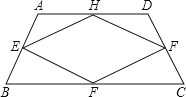
当四边形ABCD变成平行四边形时,它的中点四边形是 ;
当四边形ABCD变成矩形时,它的中点四边形是 ;
当四边形ABCD变成菱形时,它的中点四边形是 ;
当四边形ABCD变成正方形时,它的中点四边形是 ;
(3)根据以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若以一条线段为对角线作正方形,则称该正方形为这条线段的“对角线正方形”.例如,图①中正方形ABCD即为线段BD的“对角线正方形”.如图②,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA﹣AB以5cm/s的速度运动,当点P与点B不重合时,作线段PB的“对角线正方形”,设点P的运动时间为t(s),线段PB的“对角线正方形”的面积为S(cm2).
(1)如图③,借助虚线的小正方形网格,画出线段AB的“对角线正方形”.
(2)当线段PB的“对角线正方形”有两边同时落在△ABC的边上时,求t的值.
(3)当点P沿折线CA﹣AB运动时,求S与t之间的函数关系式.
(4)在整个运动过程中,当线段PB的“对角线正方形”至少有一个顶点落在∠A的平分线上时,直接写出t的值.



-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(
 ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面各问题中给出的两个变量x,y,其中y是x的函数的是
① x是正方形的边长,y是这个正方形的面积;
② x是矩形的一边长,y是这个矩形的周长;
③ x是一个正数,y是这个正数的平方根;
④ x是一个正数,y是这个正数的算术平方根.
A. ①②③B. ①②④C. ②④D. ①④
相关试题

