【题目】“五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.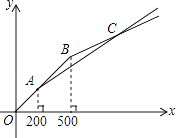
(1)求在甲商店购物时y与x之间的函数关系;
(2)两种购物方式对应的函数图象如图所示,求交点C的坐标;
(3)根据图象,请直接写出“五一”期间选择哪家商店购物更优惠.
参考答案:
【答案】
(1)解:当0≤x≤200时,y1=x,
当x>200时,y1=0.7(x﹣200)+200=0.7x+60.
(2)解:直线BC解析式为y=0.5(x﹣500)+500=0.5X+250,
由 ![]() 解得
解得 ![]() ,
,
∴点C坐标(950,725).
(3)解:由图象可知,0≤x≤200或x=950时,选择甲、乙两家费用一样.
200<x<950时,选择甲费用优惠,
x>950时,选择乙费用优惠.
【解析】(1)当0≤x≤200时,y1=x;当x>200时,由题意可知y1=0.7(x﹣200)+200;(2)根据题意在乙商店购物时y与x之间的函数关系y=0.5(x﹣500)+500;根据两种购物方式对应的函数图象,求交点C的坐标时,联立两解析式,求出的x、y的值,就是交点C的坐标;(3)根据图象可知,0≤x≤200或x=950时,选择甲、乙两家费用一样;200<x<950时,选择甲费用优惠,x>950时,选择乙费用优惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小华剪了两条宽为1的纸条,交叉叠放在一起,且它们较小的交角为60°,则它们重叠部分的面积为( )

A. 3 B. 2 C.
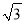 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
 (k≠0)的图象经过点(1,﹣k+2).
(k≠0)的图象经过点(1,﹣k+2).(1)求这个反比例函数的表达式;
(2)若(a,y1),(a+1,y2)是这个反比例函数图象上同一象限内的两个点,请比较y1、y2的大小,并说明理由.
-
科目: 来源: 题型:
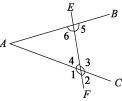
查看答案和解析>>【题目】如图,(1)∠1,∠2,∠3,∠4,∠5,∠6是直线______,______被第三条直线_______所截而成的;
(2)∠2的同位角是______,∠1的同位角是 _________;
(3)∠3的内错角是______,∠4的内错角是 _________;
(4)∠6的同旁内角是______________,∠5的同旁内角是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知点
 是
是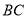 外一点,连接
外一点,连接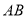 ,
,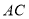 .求
.求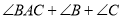 的度数.
的度数.请补充下面的推理过程:
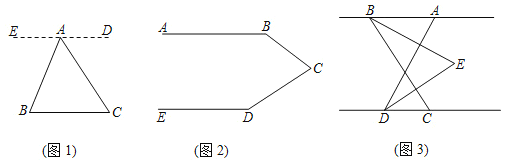
解:过点
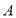 作
作 ,所以
,所以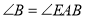 ,
, _______.
_______.又因为
 °,所以
°,所以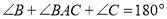 .
.(2)如图2,已知
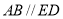 ,借鉴(1)的方法,求
,借鉴(1)的方法,求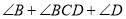 的度数;
的度数;(3)如图3,已知
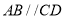 ,
, .
.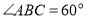 ,
,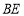 平分
平分 ,
, 平分
平分 ,
,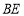 ,
, 所在的直线交于点
所在的直线交于点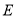 ,点
,点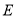 在
在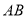 与
与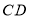 两条平行线之间,借鉴(1)的方法,求
两条平行线之间,借鉴(1)的方法,求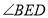 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数
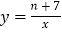 的图象的一支在第一象限,A(﹣1,a)、B(﹣3,b)均在这个函数的图象上.
的图象的一支在第一象限,A(﹣1,a)、B(﹣3,b)均在这个函数的图象上.(1)图象的另一支位于什么象限?常数n的取值范围是什么?
(2)试比较a、b的大小;
(3)作AC⊥x轴于点C,若△AOC的面积为5,求这个反比例函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数
0
1
2
3
4
5(含5次以上)
累计车费
0
0.5
0.9
a
b
1.5
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数
0
1
2
3
4
5
人数
5
15
10
30
25
15
(Ⅰ)写出a,b的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由.
相关试题

