【题目】已知某校女子田径队23人年龄的平均数和中位数都是13岁,但是后来发现其中一位同学的年龄登记错误,将14岁写成15岁,经重新计算后,正确的平均数为a岁,中位数为b岁,则下列结论中正确的是( )
A.a<13,b=13
B.a<13,b<13
C.a>13,b<13
D.a>13,b=13
参考答案:
【答案】A
【解析】解:∵原来的平均数是13岁,
∴13×23=299(岁),
∴正确的平均数a= ![]() ≈12.96<13,
≈12.96<13,
∵原来的中位数13岁,将14岁写成15岁,最中间的数还是13岁,
∴b=13;
故选:A.
【考点精析】解答此题的关键在于理解算术平均数的相关知识,掌握总数量÷总份数=平均数.解题关键是根据已知条件确定总数量以及与它相对应的总份数,以及对中位数、众数的理解,了解中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按照下列要求画图并填空:
(1)画出边
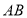 的高,垂足为
的高,垂足为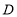 ,则点
,则点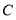 到直线
到直线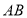 的距离是线段______的长.
的距离是线段______的长.(2)用直尺和圆规作出
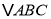 的边
的边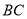 的垂直平分线
的垂直平分线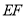 ,分别交直线
,分别交直线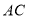 、
、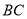 于点
于点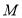 、
、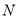 ,联结
,联结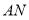 ,则线段
,则线段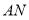 是
是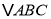 的______(保留作图痕迹).
的______(保留作图痕迹).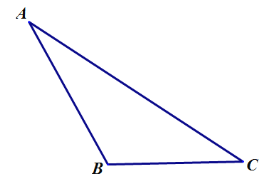
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,BD平分
,BD平分 ,交AC于点D,DE⊥AB,E为AB的中点,且DE=10cm,则AC=___.
,交AC于点D,DE⊥AB,E为AB的中点,且DE=10cm,则AC=___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣5),C(6,0)
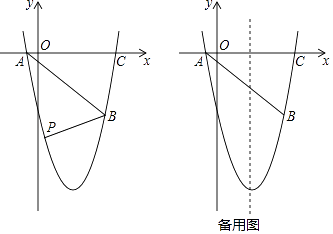
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)若点Q为抛物线的对称轴上的一个动点,试指出使△QAB为等腰三角形的点Q一共有几个?并请你求出其中一个点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,FG∥EB,∠2=∠3,那么∠EDB+∠DBC等于多少度?为什么?

解:因为FG∥EB(已知),
所以
 (__________).
(__________).因为
 (已知),
(已知),所以
 (___________).
(___________).所以DE∥BC (__________).
所以
 ______(__________).
______(__________). -
科目: 来源: 题型:
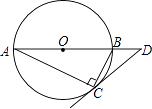
查看答案和解析>>【题目】如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
A.25°
B.40°
C.50°
D.65° -
科目: 来源: 题型:
查看答案和解析>>【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.
相关试题

