【题目】【倾听理解】（这是习题讲评课上师生围绕一道习题的对话片断）

如图，在半径为2的扇形AOB中，∠AOB＝90°，点C是弧AB上的一个动点(不与A、B重合)，OD⊥BC，OE⊥AC，垂足分别为D、E.

师：当BD＝1时，同学们能求哪些量呢？

生1：求BC、OD的长．

生2：求、的长．

……

师：正确！老师还想追问的是：去掉“BD＝1”，大家能提出怎样的问题呢？

生3：求证：DE的长为定值．

生4：连接AB，求△ABC面积的最大值．

……

师：你们设计的问题真精彩，解法也很好！

【一起参与】

（1）求“生2”的问题:“当BD＝1时，求、的长”；

（2）选择“生3”或“生4”提出的一个问题，并给出解答．

参考答案：

【答案】（1）的长为π；（2）的长为π；（2）见解析

【解析】试题分析：

（1）如图：

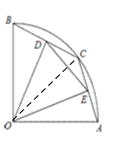
连接OC，当BD=1时，由“垂径定理”可得BC=2，从而可证△OBC为等边三角形，得到∠BOC=60°，∠AOC=30°，就可以由弧长公式求两条弧的长了；

（2）①“生3的问题”，如图：

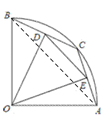
连接AB，在Rt△AOB中，由已知易得，由已知和“垂径定理”可得D、E分别是BC和AC的中点，从而可得DE是△OAB的中位线，由“三角形中位线定理”可得DE=AB=；

②“生4的问题”，如图：

由①可知， ，OC=2，当点C为的中点时，OC⊥AB，此时OF最短为，CF最长为，△ABC面积最大；

试题解析：

（1）连OC，当BD＝1时，

∵OD⊥BC

∴BC＝2BD＝2，∴△OBC是等边三角形．∴∠BOC＝60°，∴∠AOC＝30°，

∴的长为， 的长为．

（2）生3的问题：连结AB，在Rt△AOB中，AB＝，

∴DE＝AB＝．

生4的问题：∵当点C为的中点时，OC⊥AB，此时OF最短，

∴ 当点C为中点时，CF最长，由AB=是定值，可知此时，△ABC面积最大，

∵OC⊥AB，

∴OF=AB=，

∴CF=2-，

∴S△ABC最大=.

关闭