Question

【题目】已知△ABC内接于⊙O，AC是⊙O的直径，D是的中点．过点D作CB的垂线，分别交CB、CA延长线于点F、E．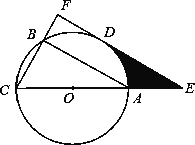

（1）判断直线EF与⊙O的位置关系，并说明理由；
（2）若CF=6，∠ACB=60°，求阴影部分的面积．

Answer 1

【答案】（1）直线EF与圆O相切（2）8-

【解析】试题分析：(1)、首先根据直径所对的圆周角为直角得出∠ABC=∠F=90°，从而得出AB∥EF，根据弧的中点得出OD⊥AB，从而根据平行线得出OD⊥EF，从而得出切线；(2)、首先根据Rt△CEF的勾股定理求出CE、EF和CF的长度，然后根据题意得出△ODE和△CEF相似求出DE的长度，最后根据阴影部分的面积等于△ODE的面积减去扇形OAD的面积求出答案.

试题解析：（1）直线EF与圆O相切，

理由为： 连接OD，如图所示： ∵AC为圆O的直径，∴∠CBA=90°， 又∵∠F=90°，
∴∠CBA=∠F=90°， ∴AB∥EF， ∴∠AMO=∠EDO， 又∵D为的中点，
∴， ∴OD⊥AB， ∴∠AMO=90°， ∴∠EDO=90°， 则EF为圆O的切线；
（2）在Rt△CEF中，∠ACB=60°，∴∠E=30°， 又∵CF=6， ∴CE=2CF=12，
根据勾股定理得：EF==6，
在Rt△ODE中，∠E=30°， ∴OD=OE，又OA=OE， ∴OA=AE=OC=CE=4，OE=8，
又∵∠ODE=∠F=90°，∠E=∠E， ∴△ODE∽△CFE， ∴， 即，

解得：DE=4， 又∵Rt△ODE中，∠E=30°， ∴∠DOE=60°，
则S阴影=S△ODE-S扇形OAD=×4×4-=8-