【题目】观察下面的三行单项式
x,2x2,4x3,8x4,16x5…①
﹣2x,4x2,﹣8x3,16x4,﹣32x5…②
2x,﹣3x2,5x3,﹣9x4,17x5…③
根据你发现的规律,完成以下各题:
(1)第①行第8个单项式为 ;第②行第2020个单项式为 .
(2)第③行第n个单项式为 .
(3)取每行的第9个单项式,令这三个单项式的和为A.计算当x=![]() 时,256(A+
时,256(A+![]() )的值.
)的值.
参考答案:
【答案】(1)27x8;22020x2020;(2)(﹣1)n﹣1(2n﹣1+1)xn;(3)64![]()
【解析】
(1)观察所给的第①与②行的式子可得它们的特点,第①行中第n个数是2n﹣1xn,第②行中第n个数是(﹣2)nxn;
(2)观察第③行式子的特点,可得第n个数是(﹣1)n﹣1(2n﹣1+1)xn,即可求出解;
(3)先求出A=28x9+(﹣2)9x9+(28+1)x9,再将x=![]() 代入求出A,最后再求256(A+
代入求出A,最后再求256(A+![]() )即可.
)即可.
解:(1)根据第①行式子的特点可得,第n个数是2n﹣1xn,
∴第8个单项式是27x8;
根据第②行式子的特点可得,第n个数是(﹣2)nxn,
∴第2020个单项式是22020x2020;
故答案为:27x8;22020x2020;
(2)根据第③行式子的特点可得,第n个数是(﹣1)n﹣1(2n﹣1+1)xn,
故答案为:(﹣1)n﹣1(2n﹣1+1)xn;
(3)第①行的第9个单项式是28x9,第②行的第9个单项式是(﹣2)9x9,第③行的第9个单项式是(28+1)x9,
∴A=28x9+(﹣2)9x9+(28+1)x9,
当x=![]() 时,A=28×(
时,A=28×(![]() )9+(﹣2)9×(
)9+(﹣2)9×(![]() )9+(28+1)×(
)9+(28+1)×(![]() )9=
)9=![]() ﹣1+
﹣1+![]() +(
+(![]() )9=(
)9=(![]() )9,
)9,
∴256(A+![]() )=256×[(
)=256×[(![]() )9+
)9+![]() ]=64
]=64![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
,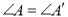 ,若
,若 ,则还需添加的一个条件有( )
,则还需添加的一个条件有( )

A.
 种B.
种B. 种C.
种C. 种D.
种D. 种
种 -
科目: 来源: 题型:
查看答案和解析>>【题目】黑板上写有1,
 ,
, ,
, ,…,
,…, 共100个数字,每次操作先从黑板上的数中选取2个数a,b,然后删去a,b,并在黑板上写上数a+b+1,则经过_____次操作后,黑板上只剩下一个数,这个数是_____.
共100个数字,每次操作先从黑板上的数中选取2个数a,b,然后删去a,b,并在黑板上写上数a+b+1,则经过_____次操作后,黑板上只剩下一个数,这个数是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知射线OB平分∠AOC,∠AOC的余角比∠BOC小42°.
(1)求∠AOB的度数:
(2)过点O作射线OD,使得∠AOC=4∠AOD,请你求出∠COD的度数
(3)在(2)的条件下,画∠AOD的角平分线OE,则∠BOE= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是
 的角平分线,
的角平分线, ,
, ,垂足分别为点E、点F,连接EF与AD相交于点O,下列结论不一定成立的是
,垂足分别为点E、点F,连接EF与AD相交于点O,下列结论不一定成立的是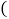


A.
 B.
B. 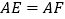 C.
C. 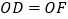 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:当点C在线段AB上,AC=nAB时,我们称n为点C在线段AB上的点值,记作dC﹣AB=n.理解:如点C是AB的中点时,即AC=
 AB,则dC﹣AB=
AB,则dC﹣AB= ;反过来,当dC﹣AB=
;反过来,当dC﹣AB= 时,则有AC=
时,则有AC= AB.因此,我们可以这样理解:dC﹣AB=n与AC=nAB具有相同的含义.
AB.因此,我们可以这样理解:dC﹣AB=n与AC=nAB具有相同的含义.
应用:(1)如图1,点C在线段AB上,若dC﹣AB=
 ,则AC= AB;若AC=3BC,则dC﹣AB= ;
,则AC= AB;若AC=3BC,则dC﹣AB= ;(2)已知线段AB=10cm,点P、Q分别从点A和点B同时出发,相向而行,当点P到达点B时,点P、Q均停止运动,设运动时间为ts.
①若点P、Q的运动速度均为1cm/s,试用含t的式子表示dP﹣AB和dQ﹣AB,并判断它们的数量关系;
②若点P、Q的运动速度分别为1cm/s和2cm/s,点Q到达点A后立即以原速返回,则当t为何值时,dP﹣AB+dQ﹣AB=
 ?
?拓展:如图2,在三角形ABC中,AB=AC=12,BC=8,点P、Q同时从点A出发,点P沿线段AB匀速运动到点B,点Q沿线段AC,CB匀速运动至点B.且点P、Q同时到达点B,设dP﹣AB=n,当点Q运动到线段CB上时,请用含n的式子表示dQ﹣CB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE=DF,若∠BED=140°,则∠BFD的度数是( )

A. 40°B. 50°C. 60°D. 70°
相关试题

