【题目】如图,已知二次函数y=![]() x2+
x2+![]() x1的图象与x轴交于A、B两点,与y轴交于点C,连接AC,点P是抛物线上的一个动点,记△APC的面积为S,当S=2时,相应的点P的个数是______.
x1的图象与x轴交于A、B两点,与y轴交于点C,连接AC,点P是抛物线上的一个动点,记△APC的面积为S,当S=2时,相应的点P的个数是______.

参考答案:
【答案】2
【解析】
先确定A点坐标为(-3,0),B点坐标为(1,0),C点坐标为(0,-1),讨论:由于S△ABC=![]() ×4×1=2,所以在x上方,抛物线上一定有两点满足△APC的面积为2;当点P在x轴下方,设P点坐标为(x,y),作PD⊥x轴于D,利用S△APC=S梯形APDO-S△PDC-S△AOC得到3y+x+7=0,而y=
×4×1=2,所以在x上方,抛物线上一定有两点满足△APC的面积为2;当点P在x轴下方,设P点坐标为(x,y),作PD⊥x轴于D,利用S△APC=S梯形APDO-S△PDC-S△AOC得到3y+x+7=0,而y=![]() x2+
x2+![]() x1,所以x2+3x+4=0,此方程无实数根,可判断在x下方,不存在抛物线上一点P满足△APC的面积为2.
x1,所以x2+3x+4=0,此方程无实数根,可判断在x下方,不存在抛物线上一点P满足△APC的面积为2.
∵令x=0,y=-1;令y=0,![]() x2+
x2+![]() x1=0,解得x1=-3,x2=1,
x1=0,解得x1=-3,x2=1,
∴A点坐标为(-3,0),B点坐标为(1,0),C点坐标为(0,-1),
连结OB,
∵S△ABC=![]() ×4×1=2,
×4×1=2,
∴在x上方,抛物线上一定有两点满足△APC的面积为2;
当点P在x轴下方,设P点坐标为(x,y),(y<-1),如图,作PD⊥x轴于D,
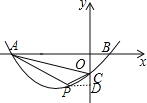
∵S△APC=S梯形APDO-S△PDC-S△AOC,
∴![]() (3-x)(-y)-
(3-x)(-y)-![]() (-1-y)(-x)-
(-1-y)(-x)-![]() ×3×1=2,
×3×1=2,
∴3y+x+7=0,
而y=![]() x2+
x2+![]() x1,
x1,
∴x2+3x+4=0,
∵△=9-4×4<0,
∴此方程无实数根,
即在x下方,不存在抛物线上一点P满足△APC的面积为2.
故答案为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E是CD的中点,连接BE并延长交AD延长线于点F.
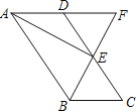
(1)求证:点D是AF的中点;
(2)若AB=2BC,连接AE,试判断AE与BF的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB<AD,∠D=30°,CD=4,以AB为直径的⊙O交BC于点E,则阴影部分的面积为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店老板去图书批发市场购买某种图书,第一次用500元购书若干本,很快售完由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用900元所购该书的数量比第一次的数量多了10本.
(1)求第一次购书每本多少元?
(2)如果这两次所购图书的售价相同,且全部售完后总利润不低于25%,那么每本图书的售价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】全善学校为了提高学生综合能力,培养学生兴趣,决定开设以下精品校本课程:A. 创新与实践,B. 数学之美,C.英美文学鉴赏,D. 小小外交家,为了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
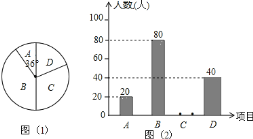
(1)这次被调查的学生共有______人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的小小外交家的课堂学习中,有三男一女四名同学表现优秀,现决定从这四名同学中任选两名参加全国英语口语大赛,求恰好选到一男一女两位同学的概率(用树状图或列表法解答).
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,O为坐标原点,点A(3,4),点B(6,0).
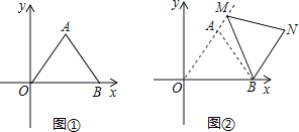
(1)如图①,求AB的长;
(2)如图2,把图①中的△ABO绕点B顺时针旋转,使O的对应点M恰好落在OA的延长线上,N是点A旋转后的对应点;
①求证:四边形AOBN是平行四边形;
②求点N的坐标.
(3)点C是OB的中点,点D为线段OA上的动点,在△ABO绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围.(直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3).
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点A1、B1、C1的坐标;
(2)若△A2B2C2是由△ABC平移而得,且点A2的坐标为(-4,4),请写出B2和C2的坐标.

相关试题

