【题目】平面直角坐标系中,O为坐标原点,点A(3,4),点B(6,0).
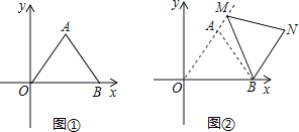
(1)如图①,求AB的长;
(2)如图2,把图①中的△ABO绕点B顺时针旋转,使O的对应点M恰好落在OA的延长线上,N是点A旋转后的对应点;
①求证:四边形AOBN是平行四边形;
②求点N的坐标.
(3)点C是OB的中点,点D为线段OA上的动点,在△ABO绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围.(直接写出结果)
参考答案:
【答案】(1)AB的长是5;(2)①见解析;②点N坐标为(9,4);(3)线段CP长的取值范围为![]() ≤CP≤9.
≤CP≤9.
【解析】
(1)根据平面直角坐标系中任意两点的距离公式计算即可;
(2)①根据平面直角坐标系中任意两点的距离公式计算出OA,从而得出OA=AB,然后根据等边对等角可得∠AOB=∠ABO,根据旋转的性质可得BM=BO,BN=BA,∠MBN=∠ABO=∠AOB,然后证出AO∥BN且AO=BN即可证出结论;
②证出AN∥x轴,再结合平行四边形的边长和点A的坐标即可得出结论;
(3)连接BP,根据题意,先根据三角形的三边关系可得当点P在线段OB上时,CP=BP-BC最短;当点P在线段OB延长线上时,CP=BP+BC最长,然后求出BP的最小值和最大值即可求出CP的最值,从而得出结论.
(1)∵点A(3,4),点B(6,0)
∴AB=![]() =5
=5
∴AB的长是5.
(2)①证明:∵OA=![]() =5
=5
∴OA=AB
∴∠AOB=∠ABO
∵△ABO绕点B顺时针旋转得△NBM
∴BM=BO,BN=BA,∠MBN=∠ABO=∠AOB
∴∠OMB=∠AOB,OA=BN
∴∠OMB=∠MBN
∴AO∥BN且AO=BN
∴四边形AOBN是平行四边形
②如图1,连接AN

∵四边形AOBN是平行四边形
∴AN∥OB即AN∥x轴,AN=OB=6
∴xN=xA+6=3+6=9,yN=yA=4
∴点N坐标为(9,4)
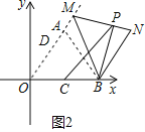
(3)连接BP
∵点D为线段OA上的动点,OA的对应边为MN
∴点P为线段MN上的动点
∴点P的运动轨迹是以B为圆心,BP长为半径的圆
∵C在OB上,且CB=![]() OB=3
OB=3
∴当点P在线段OB上时,CP=BP-BC最短;当点P在线段OB延长线上时,CP=BP+BC最长
如图2,当BP⊥MN时,BP最短
∵S△NBM=S△ABO,MN=OA=5
∴![]() MNBP=
MNBP=![]() OByA
OByA
∴BP=![]()
∴CP最小值=![]() -3=
-3=![]()
当点P与M重合时,BP最大,BP=BM=OB=6
∴CP最大值=6+3=9
∴线段CP长的取值范围为![]() ≤CP≤9.
≤CP≤9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店老板去图书批发市场购买某种图书,第一次用500元购书若干本,很快售完由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用900元所购该书的数量比第一次的数量多了10本.
(1)求第一次购书每本多少元?
(2)如果这两次所购图书的售价相同,且全部售完后总利润不低于25%,那么每本图书的售价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=
 x2+
x2+ x1的图象与x轴交于A、B两点,与y轴交于点C,连接AC,点P是抛物线上的一个动点,记△APC的面积为S,当S=2时,相应的点P的个数是______.
x1的图象与x轴交于A、B两点,与y轴交于点C,连接AC,点P是抛物线上的一个动点,记△APC的面积为S,当S=2时,相应的点P的个数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】全善学校为了提高学生综合能力,培养学生兴趣,决定开设以下精品校本课程:A. 创新与实践,B. 数学之美,C.英美文学鉴赏,D. 小小外交家,为了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
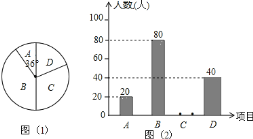
(1)这次被调查的学生共有______人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的小小外交家的课堂学习中,有三男一女四名同学表现优秀,现决定从这四名同学中任选两名参加全国英语口语大赛,求恰好选到一男一女两位同学的概率(用树状图或列表法解答).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3).
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点A1、B1、C1的坐标;
(2)若△A2B2C2是由△ABC平移而得,且点A2的坐标为(-4,4),请写出B2和C2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB:
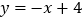 与直线AC:
与直线AC: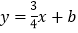 都与双曲线
都与双曲线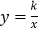 交于点A(1,m),这两条直线分别与
交于点A(1,m),这两条直线分别与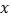 轴交于B、C两点.
轴交于B、C两点.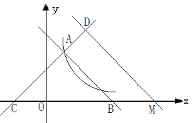
(1)求
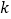 和
和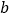 的值.
的值.(2)将直线AB沿
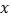 轴正方向平移,平移后交直线AC于点D,交
轴正方向平移,平移后交直线AC于点D,交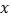 轴于点M,已知M的横坐标为6,求△MCD的面积.
轴于点M,已知M的横坐标为6,求△MCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x的一次函数,且当x=-4,y=9;当x=6时,y=-1.
(1)求这个一次函数的解析式和自变量x的取值范围;
(2)当x=-
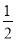 时,函数y的值;
时,函数y的值;(3)当y=7时,自变量x的值.
相关试题

