【题目】如图,用同样规格的黑白两色的正方形瓷砖铺设长方形地面,观察下列图形并解答问题.
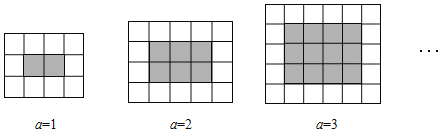
(1)在第a个图中,共有 块白瓷砖和 块黑瓷砖(用含a的代数式表示);
(2)若按上图的方式铺一块长方形地面共用了420块瓷砖,求此时a的值;
(3)已知白瓷砖每块6元,黑瓷砖每块8元,某工厂按如图方式铺设厂房地面,其中黑瓷砖的费用比白瓷砖的费用多924元,问白瓷砖和黑瓷砖各用了多少块?
参考答案:
【答案】(1)4a+6,a(a+1);(2)18;(3)白瓷砖和黑瓷砖分别用了54、156块.
【解析】
(1)首先观察图形,根据第a个图形的黑瓷砖的每行有(a+1)个,每列有a个,黑瓷砖的数量为a(a+1),然后根据横行和竖行的瓷砖求出总数,即可得出白瓷砖的块数;
(2)根据图形列出方程解得即可;
(3)由(1)得出工厂所用黑瓷砖和白瓷砖的费用,然后依题意列出方程,解得即可.
(1)根据第a个图形的黑瓷砖的每行有(a+1)个,每列有a个,黑瓷砖的数量为a(a+1),
∵图形每一横行有a+3块瓷砖,每一竖行有a+2块瓷砖,所以总块数为(a+2)(a+3),
∴白瓷砖块数为:(a+2)(a+3)﹣a(a+1)=4a+6.
故答案为:4a+6;a(a+1),
(2)结合图形易得:(a+2)(a+3)=420,
解得:a1=18,a2=﹣23(不合题意舍去)
∴按图的方式铺一块长方形地面共用了420块瓷砖时a的值为18.
(3)由(1)得:工厂所用黑瓷砖的费用为8a(a+1)元,白瓷砖的费用为6(4a+6)元.
依题意得:8a(a+1)﹣6(4a+6)=924
解得:a1=12,a2=﹣10(不合题意舍去)
黑瓷砖块数=a(a+1)=156,
白瓷砖块数=4a+6=54,
答:白瓷砖和黑瓷砖分别用了54、156块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.
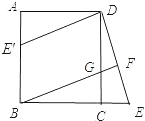
(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由。
-
科目: 来源: 题型:
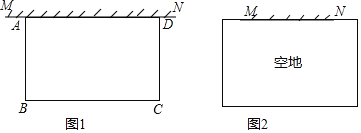
查看答案和解析>>【题目】空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.
(1)已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图1,求所利用旧墙AD的长;
(2)已知0<α<50,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx过点B(1,﹣3),对称轴是直线x=2,且抛物线与x轴的正半轴交于点A.
(1)求抛物线的解析式,并根据图象直接写出当y≤0时,自变量x的取值范图;
(2)在第二象限内的抛物线上有一点P,当PA⊥BA时,求△PAB的面积.

-
科目: 来源: 题型:
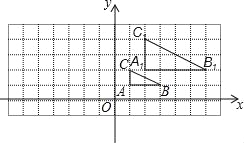
查看答案和解析>>【题目】如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1.
(1)△A1B1C1与△ABC的位似比是 ;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)设点P(a,b)为△ABC内一点,则依上述两次变换后,点P在△A2B2C2内的对应点P2的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.

(1)求证:△CAE∽△CBF
(2)若BE=1,AE=2,求CE的长.
-
科目: 来源: 题型:
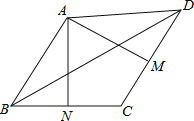
查看答案和解析>>【题目】在四边形ABCD中,M、N分别是CD、BC的中点, 且AM⊥CD,AN⊥BC,已知∠MAN=74°,∠DBC=41°,则∠ADB度数为( ).
A.15°B.17°
C.16°D.32°
相关试题

