【题目】小刚与小明在玩数字游戏,现有5张写着不同数字的卡片(如图),小刚请小明按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上的数字乘积最大,如何抽取?最大值是多少?
(2)从中取出2张卡片,使这2张卡片上的数字相除的商最小,如何抽取?最小值是多少?
(3)从中取出4张卡片,用学过的运算方法,使结果为24,如何抽取?写出运算式子(一种即可).
参考答案:
【答案】(1)15;(2)-5;(3)答案不唯一,如[-(+3)+(-5)]×[(-1)2-(+4)]=24.
【解析】
(1)抽取两个数字,使得之积最大即可;
(2)抽取两个数字,使得之商最小即可;
(3)抽取两个数字,利用“24”点游戏规则列出算式即可.
解:(1)根据题意得,-(+3)×(-5)=15.
则抽取卡片上的数字分别为-(+3)和-5这2张,积的值最大,最大值为 15;
(2)根据题意得:-5÷(-1)2
则抽取卡片上的数字分别为-5和(-1)2这2张,商的值最小,最小值为-5;
(3) [-(+3)+(-5)]×[(-1)2-(+4)]=24(答案不唯一).
-
科目: 来源: 题型:
查看答案和解析>>【题目】读题画图计算并作答
画线段AB=3 cm,在线段AB上取一点K,使AK=BK,在线段AB的延长线上取一点C,使AC=3BC,在线段BA的延长线取一点D,使AD=
 AB.
AB.(1)求线段BC、DC的长?
(2)点K是哪些线段的中点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线y=
 x与抛物线交于A、B两点,直线l为y=﹣1.
x与抛物线交于A、B两点,直线l为y=﹣1.(1)求抛物线的解析式;
(2)在l上是否存在一点P,使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.
(3)知F(x0,y0)为平面内一定点,M(m,n)为抛物线上一动点,且点M到直线l的距离与点M到点F的距离总是相等,求定点F的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D,E在圆上,四边形BCDE为矩形,这个矩形的面积是( )

A. 2 B.
 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高学生的爱国意识,陶冶爱国情操,某中学举行了以“厉害了,我的国”为主题的书法绘画大赛,该校九年级共有三个班都参加了这次活动,三个班根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分100分)如下表所示:
收集数据:

数据
(1)请填写下表:
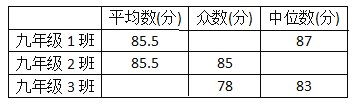
得出结论:
(2)如果在每个班级参加决赛的选手中分别选出3人参加总决赛,你认为哪个班级的实力更强一些?请简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图案是某大院窗格的一部分,其中“
 ”代表窗纸上所贴的剪纸,求:
”代表窗纸上所贴的剪纸,求: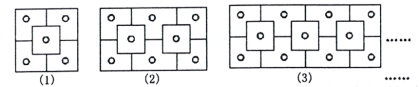
(1)第1个图中所贴剪纸“
 ”的个数为 个,第2个图中所贴剪纸“
”的个数为 个,第2个图中所贴剪纸“ ”的个数为 个,第3个图中所贴剪纸“
”的个数为 个,第3个图中所贴剪纸“ ”的个数为 个;
”的个数为 个;(2)第
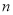 个图中所贴剪纸“
个图中所贴剪纸“ ”的个数为多少个?
”的个数为多少个?(3)如果所贴剪纸“
 ”的个数为2018个时,那么它是第几个图?
”的个数为2018个时,那么它是第几个图? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:

(1)乙队开挖到30m时,用了_____ h. 开挖6h时甲队比乙队多挖了____ m;
(2)请你求出:
①甲队在
 的时段内,y与x之间的函数关系式;
的时段内,y与x之间的函数关系式;②乙队在
 的时段内,y与x之间的函数关系式;
的时段内,y与x之间的函数关系式;(3)当x 为何值时,甲、 乙两队在 施工过程中所挖河渠的长度相等?
相关试题

