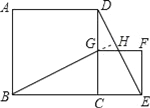
【题目】如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系.

(1)猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系;
(2)将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度a,得到如图2、如图3情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图2证明你的判断.
参考答案:
【答案】(1)BH⊥DE,即BG⊥DE,理由见解析.
(2)BG=DE,BG⊥DE仍然成立,理由见解析.
【解析】试题分析:(1)根据正方形的性质,显然三角形BCG顺时针旋转90°即可得到三角形DCE,从而判断两条直线之间的关系;
(2)结合正方形的性质,根据SAS仍然能够判定△BCG≌△DCE,从而证明结论.
解:(1)BG=DE,BG⊥DE;
∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,
∴∠BCG=∠DCE,
在△BCG和△DCE中,
BC=DC∠BCG=∠DCE CG=CE,
∴△BCG≌△DCE(SAS),
∴BG=DE;
延长BG交DE于点H,
∵△BCG≌△DCE,
∴∠CBG=∠CDE,
又∠CBG+∠BGC=90°,
∴∠CDE+∠DGH=90°,
∴∠DHG=90°,
∴BH⊥DE,即BG⊥DE;
(2)BG=DE,BG⊥DE仍然成立,
在图(2)中证明如下
∵四边形ABCD、四边形CEFG都是正方形
∴BC=CD,CG=CE,∠BCD=∠ECG=90°
∴∠BCG=∠DCE,
∴△BCG≌△DCE(SAS)
∴BG=DE,∠CBG=∠CDE,
又∵∠BHC=∠DHO,∠CBG+∠BHC=90°
∴∠CDE+∠DHO=90°
∴∠DOH=90°
∴BG⊥DE.
点睛: 能熟练运用正方形的性质和全等三角形的判定定理分析解答相关问题,正方形的性质:正方形的四条边相等,四个角都是直角;全等三角形的判定定理:有两边及夹角对应相等的两三角形全等(SAS).
-
科目: 来源: 题型:
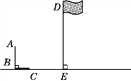
查看答案和解析>>【题目】如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】万达旅行社为吸引市民组团去黄山风景区旅游,推出了如下的收费标准:

宿州高铁新区组织员工去黄山风景区旅游,共支付给万达旅行社旅游费用27 000元,请问该单位这次共有多少员工去黄山风景区旅游?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边上的中线,点D,E分别在边AC和BC上,DB=DE,DE与BM相交于点N,EF⊥AC于点F,以下结论:
①∠DBM=∠CDE;②S△BDE<S四边形BMFE;③CD·EN=BN·BD;④AC=2DF.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校要成立一支由6名女生组成的礼仪队,八年级两个班各选6名女生,分别组成甲队和乙队参加选拔.每位女生的身高统计如图,部分统计量如下表:
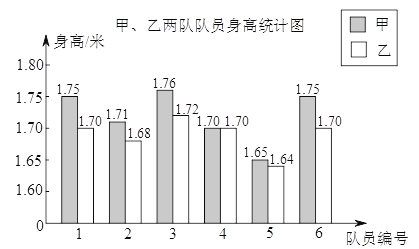
平均数
标准差
中位数
甲队
1.72
0.038
乙队
0.025
1.70
(1)求甲队身高的中位数;
(2)求乙队身高的平均数及身高不小于1.70米的频率;
(3)如果选拔的标准是身高越整齐越好,那么甲、乙两队
中哪一队将被录取?请说明理由.
-
科目: 来源: 题型:
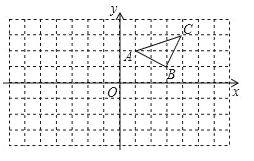
查看答案和解析>>【题目】已知:如图所示.
(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小,并直接写出此时PA+PC的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:
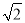 ≈1.41,
≈1.41,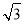 ≈1.73)
≈1.73)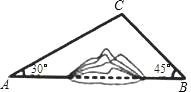
相关试题

