Question

【题目】如图，在五边形ABCDE中，∠BAE=120°，∠B=∠E=90°，AB=BC=1，AE=DE=2，在BC，DE上分别找一点M，N，使△AMN的周长最小，则△AMN的最小周长为 ．

Answer 1

【答案】2
【解析】解：作A关于BC和ED的对称点A′，A″，连接A′A″，交BC于M，交ED于N，则A′A″即为△AMN的周长最小值．过点A′作EA延长线的垂线，垂足为H，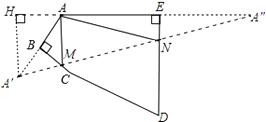

∵AB=BC=1，AE=DE=2，
∴AA′=2BA=2，AA″=2AE=4，
则Rt△A′HA中，∵∠EAB=120°，∴∠HAA′=60°，
∵A′H⊥HA，
∴∠AA′H=30°，
∴AH= AA′=1，
∴A′H= ，
A″H=1+4=5，
∴A′A″= =2 ，
所以答案是：2 ．
【考点精析】解答此题的关键在于理解轴对称-最短路线问题的相关知识，掌握已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．