【题目】解不等式(组)
(1)解不等式:1﹣ ![]() ≤
≤ ![]()
(2)不等式组  ,并将其解集在数轴上表示出来.
,并将其解集在数轴上表示出来.
参考答案:
【答案】
(1)解:1﹣ ![]() ≤
≤ ![]()
去分母,得6﹣3(x﹣2)≤2(x+1)
去括号,得6﹣3x+6≤2x+2
移项、合并同类项,得﹣5x≤﹣10,
系数化为1,得x≥2
(2)解: 
由①得:x>﹣6,
由②得:x<6,
∴原不等式组得解集为:﹣6<x<6.
在数轴上表示:
![]()
【解析】(1)去分母、去括号,然后移项、合并同类项,系数化为1,即可求得;(2)解先求出各不等式的解集,再求其公共解集即可.
【考点精析】解答此题的关键在于理解不等式的解集在数轴上的表示的相关知识,掌握不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈,以及对一元一次不等式的解法的理解,了解步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC=1,AE=DE=2,在BC,DE上分别找一点M,N,使△AMN的周长最小,则△AMN的最小周长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算2a2.3a3的结果是( )
A. 5a3 B. 6a3 C. 6a6 D. 6a9
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,DE、DF是△ABC的中位线,连接EF、AD,其交点为O.求证:

(1)△CDE≌△DBF;
(2)OA=OD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).

(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法).
(2)直接写出A′、B′、C′三点的坐标:
A′( , ); B′( , );
C′( , ).
(3)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,CE是△ABC的角平分线.
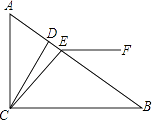
(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个图形无论经过平移变换还是旋转变换,下列结论一定正确的是________(把所有你认为正确的序号都写上)
①对应线段平行;
②对应线段相等;
③对应角相等;
④图形的形状和大小都不变.
相关试题

