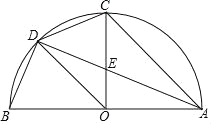
【题目】如图,AB是半圆直径,半径OC⊥AB于点O,D为半圆上一点,AC∥OD,AD与OC交于点E,连结CD、BD,给出以下三个结论:①OD平分∠COB;②BD=CD;③CD2=CECO,其中正确结论的序号是 .
参考答案:
【答案】①②③
【解析】
试题分析:①由OC⊥AB就可以得出∠BOC=∠AOC=90°,再由OC=OA就可以得出∠OCA=∠OAC=45°,由AC∥OD就可以得出∠BOD=45°,进而得出∠DOC=45°,从而得出OD平分∠COB.故①正确;
②由∠BOD=∠COD即可得出BD=CD,故②正确;
③由∠AOC=90°就可以得出∠CDA=45°,得出∠DOC=∠CDA,就可以得出△DOC∽△EDC.进而得出![]() ,得出CD2=CE·CO.故③正确.
,得出CD2=CE·CO.故③正确.
故答案为:①②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知 A=3a2﹣2a+1,B=5a2﹣3a+2,求2A﹣B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A.实数包括正实数、零、负实数B.正整数和负整数统称为整数
C.无理数一定是无限小数D.2是4的平方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某非物质文化遗产共有16名传承艺人,为了了解每位艺人的日均生产能力,随机调查了某一天每位艺人的生产件数.获得数据如下表:
生产件数(件)
10
11
12
13
14
15
人数(人)
1
6
3
3
2
1
从这一天16名艺人中随意抽取1人,则他的这一天生产件数最可能的是( )
A. 11件B. 12件C. 13件D. 15件
-
科目: 来源: 题型:
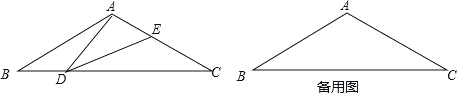
查看答案和解析>>【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】几个人共同种一批树苗,如果每人种12棵,则剩下6棵树苗未种;如果每人种15棵,则缺6棵树苗.求参与种树的人数和树苗的总数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】|32|=_____.
相关试题

