搜索
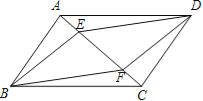
【题目】已知：如图，在ABCD中，E、F是对角线AC上的两点，且AE=CF．求证：四边形BFDE是平行四边形．
参考答案：
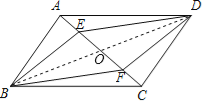
【答案】证明：连续BD交AC于点O
∵ 四边形ABCD是平行四边形
∴ AO = CD，DO = BO
∵ AE = CF
∴ AO – AE =" CO" – CF，即EO = FO
∴ 四边形EBFD是平等四边形
【解析】试题分析：先连接BD，交AC于O，由于四边形ABCD是平行四边形，易知OB=OD，OA=OC，而AE=CF，根据等式性质易得OE=OF，再根据两组对角线互相平分的四边形是平行四边形可证之．
试题解析：连接BD，交AC于O， ∵四边形ABCD是平行四边形， ∴OB=OD，OA=OC， ∵AE=CF，
∴OA﹣AE=OC﹣CF， ∴OE=OF， ∴四边形BFDE是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在数学课上，老师给出这样一个问题：
如图1，在平行四边形ABCD中，AB＜BC．利用尺规作图，在边BC上确定一点E为圆心作圆，使⊙E与边AB，AD都相切（不写作法，保留作图痕迹）；
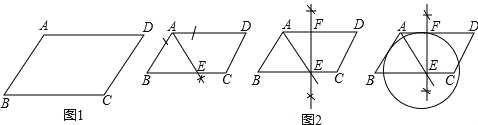
小刚是这样思考的：（如图2）
（1）作∠BAD的平分线与BC边交于点E；
（2）过点E作边AD的垂线，垂足为点F；
（3）以点E为圆心，EF长为半径作圆即可；
小刚把想法和老师交流了，得到了老师的肯定和赞扬，请你回答：小刚这样做的依据是 ．
-
科目： 来源： 题型：
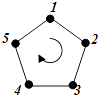
查看答案和解析>>【题目】如图，给正五边形的顶点依次编号为1，2，3，4，5．若从某一顶点开始，沿正五边形的边顺时针方向行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”．如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”．若小宇从编号为2的顶点开始，第81次“移位”后，则他所处顶点的编号是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】经过两点A(2，3)，B(－4，3)作直线AB，则直线AB( )
A. 平行于x轴 B. 平行于y轴 C. 经过原点 D. 无法确定
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）﹣9﹣2+7
（2）
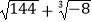
（3）
（4）﹣22﹣（1﹣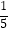
×0.2）÷（﹣2）3 -
科目： 来源： 题型：
查看答案和解析>>【题目】同一平面内的三条直线，其交点的个数可能为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课时间的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y随时间x（分钟）的变化规律如图所示（其中AB、BC分别为线段，CD为双曲线的一部分），请问：
如果有一道数学综合题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师可否在学生注意力达到较为理想的稳定状态下讲解完这道题目？
你的结论是 （填写“可以”或“不可以”），理由是 （请通过你计算所得的数据说明理由）．
相关试题
