【题目】三角形ABC中,AB=5,![]() ,BC边上的高AD=4,BC=__________
,BC边上的高AD=4,BC=__________
参考答案:
【答案】7或1
【解析】
分两种情况讨论:锐角三角形和钝角三角形,根据勾股定理求得BD,CD,再由图形求出BC,在锐角三角形中,BC=BD+CD,在钝角三角形中,BC=CD-BD.
解:(1)如图
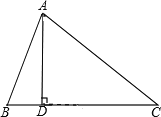
AB=5,![]() ,BC边上的高AD=4,
,BC边上的高AD=4,
在Rt△ABD中AB=5,AD=4,由勾股定理得
BD2=AB2-AD2,
∴BD=3,
在Rt△ACD中![]() ,AD=4,由勾股定理得
,AD=4,由勾股定理得
CD2=AC2-AD2,
∴CD=3,
∴BC的长为BD+DC=7;
(2)钝角△ABC中,
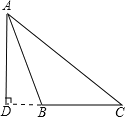
AB=5,![]() ,BC边上高AD=4,
,BC边上高AD=4,
在Rt△ABD中AB=5,AD=4,由勾股定理得
BD2=AB2-AD2=132-122=25,
∴BD=4,
在Rt△ACD中![]() ,AD=4,由勾股定理得
,AD=4,由勾股定理得
CD2=AC2-AD2,
∴CD=3,
∴BC的长为DC-BD=1.
故答案为7或1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明调查了班级里20位同学本学期购买课外书的花费情况,并将结果绘制成了如图的统计图.在这20位同学中,本学期购买课外书的花费的众数和中位数分别是( )

A. 50,50 B. 50,30 C. 80,50 D. 30,50
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知对称轴为y轴的抛物线y=ax2+bx+3,与x轴两个交点的横坐标分别为x1,x2.若点(x1,x2)在反比例函数y=
 的图象上,该抛物线与x轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k,则反比例函数y=
的图象上,该抛物线与x轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k,则反比例函数y= (x>0)的图象是( )
(x>0)的图象是( )A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),△ABC中,AB=AC,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F。
①EF与BE、CF间有怎样的数量关系?∠A与∠BOC怎样的数量关系?说明理由。
②若AB≠AC,其他条件不变,如图(2),图中还有几个等腰三角形吗?如果有,第①问中EF与BE、CF间的关系还存在吗?∠A与∠BOC的数量关系还存在吗?
③若△ABC中,AB≠AC,∠B的平分线与三角形外角∠ACG的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F。如图(3),EF与BE、CF间的关系如何?∠A与∠BOC的数量关系?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt ABC中,
 ,AB=5cm, AC=3cm, 动点P从点B出发沿射线BC以2cm/s 的速度移动,设运动的时间为t秒.t= __________ 时三角形ABP为直角三角形.
,AB=5cm, AC=3cm, 动点P从点B出发沿射线BC以2cm/s 的速度移动,设运动的时间为t秒.t= __________ 时三角形ABP为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一次函数y=mx+4m﹣2.
(1)若这个函数的图象经过原点,求m的值;
(2)若这个函数的图象不过第四象限,求m的取值范围;
(3)不论m取何实数这个函数的图象都过定点,试求这个定点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数
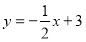 的图象 与x轴、y轴分别交于点A,B.
的图象 与x轴、y轴分别交于点A,B. 
(1)求点A,B的坐标;
(2)M为ー次函数y=x+3的图象上一点,若 △ABM与△ABO的面积相等,求点M的坐标;
(3)Q为y轴上的一点,若三角形ABQ为等腰三角形 ,请直接写出点Q的坐标.
相关试题

