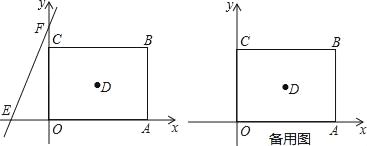
【题目】如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a、b、c分别满足﹣(a﹣4)2≥0,c=![]() +8.
+8.
(1)求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;
(2)直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
(3)点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,求![]() 的值.
的值.
参考答案:
【答案】(1)y=2x+8,D(2,2);(2)存在,5;(3)![]() .
.
【解析】
试题(1)利用非负数的性质求出a,b,c的值,进而确定出直线y=bx+c,得到正方形的边长,即可确定出D坐标;
(2)存在,理由为:对于直线y=2x+8,令y=0求出x的值,确定出E坐标,根据题意得:当直线EF平移到过D点时正好平分正方形AOBC的面积,设平移后的直线方程为y=2x+t,将D坐标代入求出b的值,确定出平移后直线解析式,进而确定出此直线与x轴的交点,从而求出平移距离,得到t的值;
过P点作PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,利用同角的余角相等得到一对角相等,再由一对直角相等,利用角平分线定理得到PH=PQ,利用AAS得到三角形OPH与三角形MPQ全等,得到OH=QM,根据四边形CNPG为正方形,得到PG=BQ=CN,由三角形CGP为等腰直角三角形得到CP=![]() GP=
GP=![]() BM,即可求出所求式子的值.
BM,即可求出所求式子的值.
试题解析:(1)∵-(a-4)2≥0,![]() ,
,
∴a=4,b=2,c=8,
∴直线y=bx+c的解析式为:y=2x+8,
∵正方形OABC的对角线的交点D,且正方形边长为4,
∴D(2,2);
(2)存在,理由为:
对于直线y=2x+8,
当y=0时,x=-4,
∴E点的坐标为(-4,0),
根据题意得:当直线EF平移到过D点时正好平分正方形AOBC的面积,
设平移后的直线为y=2x+t,
代入D点坐标(2,2),
得:2=4+t,即t=-2,
∴平移后的直线方程为y=2x-2,
令y=0,得到x=1,
∴此时直线和x轴的交点坐标为(1,0),平移的距离为1-(-4)=5,
则t=5秒;
(3)过P点作PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,
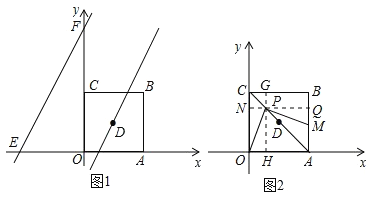
∵∠OPM=∠HPQ=90°,
∴∠OPH+∠HPM=90°,∠HPM+∠MPQ=90°,
∴∠OPH=∠MPQ,
∵AC为∠BAO平分线,且PH⊥OA,PQ⊥AB,
∴PH=PQ,
在△OPH和△MPQ中,
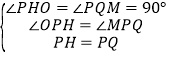 ,
,
∴△OPH≌△MPQ(AAS),
∴OH=QM,
∵四边形CNPG为正方形,
∴PG=BQ=CN,
∴CP=![]() PG=
PG=![]() BM,
BM,
即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,路边有一灯杆AB,在A点灯光的照耀下,点D处一直立标杆CD的影子为DH,沿BD方向的F处有另一标杆EF,其影子为FG,
(1)在图中画出灯杆AB,并标上相应的字母;(不写画法,保留画图痕迹)
(2)已知标杆EF=1.6m,影长FG=4m,灯杆AB到标杆EF的距离BF=8m,求灯杆AB的长.
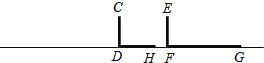
-
科目: 来源: 题型:
查看答案和解析>>【题目】两建筑物AB和CD的水平距离为30米,如图所示,从A点测得太阳落山时,太阳光线AC照射到AB后的影子恰好在CD的墙角时的角度∠ACB=60°,又过一会儿,当AB的影子正好到达CD的楼顶D时的角度∠ADE=30°,DE⊥AB于E,则建筑物CD的高是多少米?(
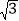 ≈1.732,结果保留两位有效数字)
≈1.732,结果保留两位有效数字)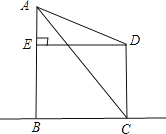
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC=______度;
(2)求∠EDF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:(1)当线段AB平行于投影面P时,它的正投影是线段A1B1,线段与它的投影的大小关系为AB
___A1B1;
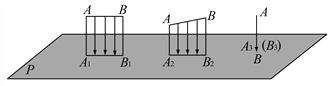
(2)当线段AB倾斜于投影面P时,它的正投影是线段A2B2,线段与它的投影的大小关系为AB___A2B2;
(3)当线段AB垂直于投影面P时,它的正投影是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为
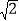 ;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )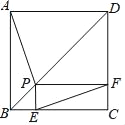
A. ①②③B. ①②④C. ②③④D. ①③④
相关试题

