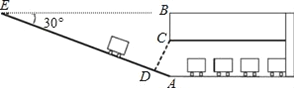
【题目】某商场为方便顾客停车，决定设计一个地下停车场，为了测得该校地下停车场的限高CD，在施工时间测得下列数据：如图，从地面E点测得地下停车场的俯角为30°，斜坡AE的长为16米，地面B点（与E点在同一个水平线）距停车场顶部C点（A、C、B在同一条直线上且与水平线垂直）1.2米．试求该校地下停车场的高度AC及限高CD（结果精确到0.1米）．

参考答案：

【答案】

【解析】试题分析：首先根据题意得出AB=8米，从而得出AC的长度，然后根据三角函数得出CD的长度.

试题解析：由题意得，AB⊥EB，CD⊥AE，∴∠CDA=∠EBA=90°，

∵∠E=30°，∴AB=AE=8米，

∵BC=1.2米，∴AC=AB﹣BC=6.8米，

∵∠DCA=90°﹣∠A=30°，∴CD=AC×cos∠DCA=6.8×≈5.9米．

答：该校地下停车场的高度AC为6.8米，限高CD约为5.9米．

关闭