【题目】已知:数轴上A、B两点表示的有理数分别为a、b,且(a﹣1)2+|b+2|=0,
(1)求(a+b)2015的值.
(2)数轴上的点C与A、B两点的距离的和为7,求点C在数轴上表示的数c的值.
![]()
参考答案:
【答案】(1)﹣1;(2)c的值是﹣4或3.见解析
【解析】
试题分析:(1)根据(a﹣1)2+|b+2|=0,可以求得a、b的值,从而可以得到(a+b)2015的值;
(2)由第(1)问中求得的a的值和数轴上的点C与A、B两点的距离的和为7,可知点C可能在点B的左侧或点C可能在点A的右侧两种情况,然后进行计算即可解答本题.
解:(1)∵(a﹣1)2+|b+2|=0,
∴a﹣1=0,b+2=0,
解得a=1,b=﹣2,
∴(a+b)2015=(1﹣2)2015=(﹣1)2015=﹣1;
(2)∵a=1,b=﹣2,数轴上A、B两点表示的有理数分别为a、b,数轴上的点C与A、B两点的距离的和为7,
∴点C可能在点B的左侧或点C可能在点A的右侧,
当点C在点B的左侧时,1﹣c+﹣2﹣c=7,得c=﹣4,
当点C在点A的右侧时,c﹣1+c﹣(﹣2)=7,得c=3,
即点C在数轴上表示的数c的值是﹣4或3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个形状、大小完全相同的含有30゜、60゜的三角板如图①放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转.
(1)直接写出∠DPC的度数.
(2)若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度(如图②),若PF平分∠APD,PE平分∠CPD,求∠EPF的度数;
(3)如图③,在图①基础上,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3゜/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2゜/秒,(当PC转到与PM重合时,两三角板都停止转动),在旋转过程中,当2∠CPD=3∠BPM,求旋转的时间是多少.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
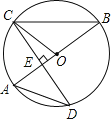
(1)求证:∠BCO=∠D;
(2)若CD=
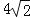 ,AE=2,求⊙O的半径.
,AE=2,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】某农户承包荒山若干亩种果树2000棵,每年需对果园投资7800元,水果年总产量为18000千克,此水果在市场上每千克售a元,在果园自助销售每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售1000千克,需3人帮忙,每人每天付工资80元,农用车运费及其他各项税费平均每天60元,假定两种方式都能将水果全部销售出去.
(1)直接写出一年中两种方式出售水果的总销售金额是多少元.(用含a,b的最简式子表示)
(2)若a=1.3元,b=1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好?
(3)为了提高收益,该农户明年准备增加投入资金加强果园管理,预计每增加投入1元,水果产量增加5千克,力争到明年纯收入达到16500元,而且该农户采用了(2)中较好的出售方式出售,销售单价与(2)一样,那么该农户要增加投资多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据5,4,2,5,6的中位数是( )
A.5 B.4 C.2 D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x分别取﹣
 、﹣
、﹣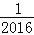 、﹣
、﹣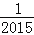 、…、﹣
、…、﹣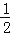 、﹣2、﹣1、0、1、2、…、2015、2016、2017时,计算分式
、﹣2、﹣1、0、1、2、…、2015、2016、2017时,计算分式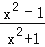 的值,再将所得结果相加,其和等于 .
的值,再将所得结果相加,其和等于 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如果获利100元记作+100元,那么支出200元记作
A、+200元 B、-200元 C、+100元 D、-100元
相关试题

