【题目】△ABC 中,已知点 D,E,F 分别是 BC,AD,CE 边上的中点,且 S△ABC=4cm2 则 S△BEF 的值为( )
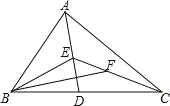
A. 2cm2 B. 1cm2 C. 0.5cm2 D. 0.25cm2
参考答案:
【答案】B
【解析】根据三角形的中线把三角形分成两个面积相等的三角形求出S△BCE=![]() S△ABC,S△BEF=
S△ABC,S△BEF=![]() S△BCE,然后代入数据进行计算即可得解.
S△BCE,然后代入数据进行计算即可得解.
∵点D、 E分别是边BC、AD上的中点,
∴S△ABD=![]() S△ABC,S△ACD=
S△ABC,S△ACD=![]() S△ABC,
S△ABC,
S△BDE=![]() S△ABD,S△CDE=
S△ABD,S△CDE=![]() S△ACD,
S△ACD,
∴S△BCE=S△BDE+S△CDE=![]() S△ABD+
S△ABD+![]() S△ACD=
S△ACD=![]() S△ABC,
S△ABC,
∵点F是边CE的中点,
∴S△BEF=![]() S△BCE=
S△BCE=![]() ×
×![]() S△ABC=
S△ABC=![]() S△ABC,
S△ABC,
∵S△ABC=4,
∴S△BFF=![]() ×4=1.
×4=1.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
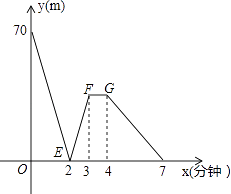
(1)A、B两点之间的距离是米,甲机器人前2分钟的速度为米/分;
(2)若前3分钟甲机器人的速度不变,求线段EF所在直线的函数解析式;
(3)若线段FG∥x轴,则此段时间,甲机器人的速度为米/分;
(4)求A、C两点之间的距离;
(5)直接写出两机器人出发多长时间相距28米. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC的周长是10,求□ABCD的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:
①∠A+∠B=∠C
②∠A:∠B:∠C=1:2:3
③∠A=
 ∠B=
∠B=  ∠C
∠C④∠A=∠B=2∠C 中,能确定△ABC 为直角三角形的条件有( )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,过点A(﹣
 ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求点D的坐标;
(4)在(3)的条件下,直线BD上是否存在点P,使以A、B、P三点为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB请你添加一个条件 , 使四边形DBCE是矩形.

相关试题

