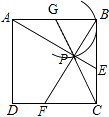
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中, ①AE和BF的位置关系为;
②线段MN的最小值为 . 
参考答案:
【答案】AE⊥BF;![]()
【解析】解:①如图,∵动点F,E的速度相同, ∴DF=CE,
又∵CD=BC,
∴CF=BE,
在△ABE和△BCF中, ,
,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠CBF,AE=BF,
∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠APB=90°,
∴AE⊥BF,②∵点P在运动中保持∠APB=90°,
∴点P的路径是一段以AB为直径的弧,
设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,
在Rt△BCG中,CG= ![]() =
= ![]() =
= ![]() ,
,
∵PG= ![]() AB=
AB= ![]() ,
,
∴CP=CG﹣PG= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
即线段CP的最小值为 ![]() ,
,
所以答案是AE⊥BF, ![]() .
.
【考点精析】利用正方形的性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在点B处,直角顶点F在CD的延长线上,BF与AD交于点G,斜边与CD交于点E
 ,若CE=1,则DG的长为( )
,若CE=1,则DG的长为( )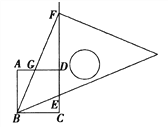
A.
 B.
B. 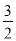 C.
C.  D. 3
D. 3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF=3,则小正方形的边长为何?( )

A.
B.
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某数学兴趣小组为了测量河对岸l1的两棵古树A、B之间的距离,他们在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则古树A、B之间的距离为m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)小宁和婷婷在一起做拼图游戏,他们用 “
 、△△、=”构思出了独特而有意义的图形并根据图形还用简洁的语言进行了表述:
、△△、=”构思出了独特而有意义的图形并根据图形还用简洁的语言进行了表述:
观察以上图案
(1)这个图案有什么特点?
(2)它可以通过一个“基本图案”经过怎样的平移而形成?
(3)在平移的过程中,“基本图案”的大小、形状、位置是否发生了变化?你能解释其中的道理吗?
-
科目: 来源: 题型:
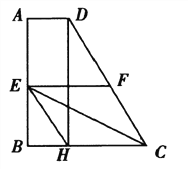
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=6,CD=8,E,F分别是边ABCD的中点, DH⊥BC于点H,连接EH,EC,EF,现有下列结论:①∠CDH=30°;②EF=4;③四边形EFCH是菱形;④S△EFC=3S△BEH.你认为结论正确的有___________.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

相关试题

