【题目】在某水果店进行了一次促销活动,一次性购买![]() 种水果的单价
种水果的单价![]() (元)与购买量
(元)与购买量![]() (千克)的函数关系如图.
(千克)的函数关系如图.
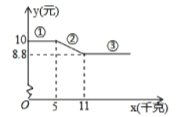
(1)当![]() 时,单价
时,单价![]() 为_______元.
为_______元.
(2)求图中第②段函数图象的解析式,并指出![]() 的取值范围.
的取值范围.
(3)促销活动期间,张老师计划去该店买![]() 种水果10千克,那么张老师共需花费多少钱?
种水果10千克,那么张老师共需花费多少钱?
参考答案:
【答案】(1)10;x≥11;(2)y=0.2x+11(5≤x≤11);(3)张老师共需花费9元.
【解析】
(1)根据观察函数图象的横坐标,纵坐标,可得答案;
(2)根据待定系数法,可得函数的解析式;
(3)根据(2)的结论解答即可.
(1)观察函数图象的横坐标,纵坐标,不超过5千克时,单价是10元,数量不少于11千克时,单价为8.8元.故答案为:10;x≥11;(2)设②段函数图象的解析式y=kx+b(k是常数,b是常数,k≠0),图象过点(5,10)(11,8.8),![]() ,解得
,解得![]() ,第②段函数图象的解析式y=0.2x+11(5≤x≤11);(3)当x=10时,y=0.2×10+11=9,答:促销活动期间,张老师计划去该店购买A种水果10千克,那么张老师共需花费9元.
,第②段函数图象的解析式y=0.2x+11(5≤x≤11);(3)当x=10时,y=0.2×10+11=9,答:促销活动期间,张老师计划去该店购买A种水果10千克,那么张老师共需花费9元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩有如下信息:
A
B
C
D
E
平均分
方差
数学
71
72
69
68
70
2
英语
88
82
94
85
76
85
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差.
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD中,对角线AC、BD交于点O,过O点的两直线OE、OF互相垂直,分别交AB、BC于E、F,连接EF.
(1)求证:OE=OF;
(2)若AE=4,CF=3,求EF的长;
(3)若AB=8cm,请你计算四边形OEBF的面积.

-
科目: 来源: 题型:
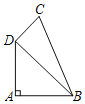
查看答案和解析>>【题目】如图,在四边形ABCD中,已知AB=AD=2,BC=3,CD=1,∠A=90°.
(1)求BD的长;
(2)求∠ADC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
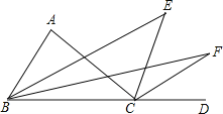
查看答案和解析>>【题目】如图,在△ABC中,∠A=80°,∠ABC与∠ACD的平分线交于点E,∠EBC与∠ECD的平分线相交于点F,则∠BFC=______.
-
科目: 来源: 题型:
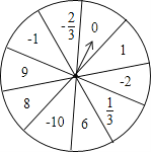
查看答案和解析>>【题目】如图,转盘被等分成10个扇形,每个扇形上面写有一个有理数.任意转动转盘,求转得下列各数的概率.
(1)转得正数;
(2)转得负整数;
(3)转得绝对值不大于5的数.
相关试题

