搜索
【题目】如图，一块直角三角形的纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（ ）.
A. 2 cm B. 4 cm C. 3 cm D. 5 cm
参考答案：
【答案】C
【解析】
根据折叠的性质可得AC=AE=6，CD=DE，∠ACD=∠AED=∠DEB=90°，利用勾股定理列式求出AB，从而求出BE，设CD=DE=x，表示出BD，然后在Rt△DEB中，利用勾股定理列式计算即可得解．
∵△ACD与△AED关于AD成轴对称，
∴AC=AE=6cm,CD=DE,
在Rt△ABC中,
∴AB=10，
∴BE=ABAE=106=4，
设CD=DE=xcm，则DB=BCCD=8x，
在Rt△DEB中,由勾股定理,得
解得x=3，即CD=3cm.
故选：C.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，AB=2，AD=5，过点A、B作⊙O，交AD，BC于点E，F，连接BE，CE，过点F作FG⊥CE，垂足为G．
（1）当点F是BC的中点时，求证：直线FG与⊙O相切；
（2）若FG∥BE时，求AE的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】某电子科技公司开发一种新产品，公司对经营的盈亏情况每月最后一天结算1次．在1～12月份中，公司前x个月累计获得的总利润y（万元）与销售时间x（月）之间满足二次函数关系式y=a（x﹣h）2+k，二次函数y=a（x﹣h）2+k的一部分图象如图所示，点A为抛物线的顶点，且点A、B、C的横坐标分别为4、10、12，点A、B的纵坐标分别为﹣16、20．
（1）试确定函数关系式y=a（x﹣h）2+k；
（2）分别求出前9个月公司累计获得的利润以及10月份一个月内所获得的利润；
（3）在前12个月中，哪个月该公司一个月内所获得的利润最多？最多利润是多少万元？ -
科目： 来源： 题型：
查看答案和解析>>【题目】等腰Rt△ACB，∠ACB＝90°，AC＝BC，点A、C分别在x轴、y轴的正半轴上．
（1）如图1，求证：∠BCO＝∠CAO
（2）如图2，若OA＝5，OC＝2，求B点的坐标
（3）如图3，点C（0，3），Q、A两点均在x轴上，且S△CQA＝18．分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM，连接MN交y轴于P点，OP的长度是否发生改变？若不变，求出OP的值；若变化，求OP的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，E为边长为1的正方形ABCD中CD边上的一动点（不含点C、D），以BE为边作图中所示的正方形BEFG．
（1）求∠ADF的度数；
（2）如图2，若BF交AD于点H，连接EH，求证：HB平分∠AHE；
（3）如图3，连接AE、CG，作BM⊥AE于点M，BM交GC于点N，连接DN．当E在CD上运动时，求证：NC=NG．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本题满分8分）
为了加强学生课外阅读，开阔视野，某校开展了“书香校园，从我做起”的主题活动．学校随机抽取了部分学生，对他们一周的课外阅读时间进行调查，绘制出频数分布表和频数分布直方图的一部分如下：
请根据图表信息回答下列问题：
（1）频数分布表中的
，
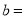；（2）将频数分布直方图补充完整；
（3）学校将每周课外阅读时间在
小时以上的学生评为“阅读之星”，请你估计该校
名学生中评为“阅读之星”的有多少人？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠1＝∠BDC，∠2＋∠3＝180°．
(1) 请你判断DA与CE的位置关系，并说明理由；
(2) 若DA平分∠BDC，CE⊥AE于点E，∠1＝70°，试求∠FAB的度数．
相关试题
