Question

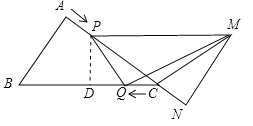
【题目】已知，如图①，在ABCD中，AB=3cm，BC=5cm，AC⊥AB，△ACD沿AC的方向匀速平移得到△PNM，速度为1cm/s；同时，点Q从点C出发，沿CB方向匀速移动，速度为1cm/s，当△PNM停止平移时，点Q也停止移动，如图②，设移动时间为t（s）（0＜t＜4），连接PQ，MQ，MC，解答下列问题：

（1）当t为何值时，PQ∥MN？

（2）设△QMC的面积为y（cm2），求y与x之间的函数关系式；

（3）是否存在某一时刻t，使S△QMC：S四边形ABQP=1：4？若存在，求出t的值；若不存在，请说明理由．

（4）是否存在某一时刻t，使PQ⊥MQ？若存在，求出t的值；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）（0＜t＜4）；（3）t=2；（4）．

【解析】

试题分析：（1）根据勾股定理求出AC，根据PQ∥AB，得出，，求解即可；

（2）过点P作PD⊥BC于D，根据△CPD∽△CBA，得出，求出PD=，再根据S△QMC=S△QPC，得出y=S△QMC=QCPD，再代入计算即可；

（3）根据S△QMC：S四边形ABQP=1：4，得出S△QPC：S△ABC=1：5，代入得出（）：6=1：5，再计算即可；

（4）根据PQ⊥MQ得出△PDQ∽△MQP，得出=MPDQ，根据勾股定理得出=MPDQ，再分别代入得出，求出t即可．

试题解析：（1）在Rt△ABC中，AC==4，由平移的性质得MN∥AB，∵PQ∥MN，∴PQ∥AB，∴，∴，解得；

（2）过点P作PD⊥BC于D，∵△CPD∽△CBA，∴，∴，∴PD=，∵PD∥BC，∴S△QMC=S△QPC，∴，即（0＜t＜4）；

（3）∵S△QMC：S四边形ABQP=1：4，∴S△QPC：S四边形ABQP=1：4，∴S△QPC：S△ABC=1：5，（）：6=1：5，整理得：，解得；

（4）若PQ⊥MQ，则∠PQM=∠PDQ，∵∠MPQ=∠PQD，∴△PDQ∽△MQP，∴，∴=MPDQ，∴=MPDQ，∵CD=，∴DQ=CD﹣CQ==，∴，∴整理得，解得（舍去），，∴时，PQ⊥MQ．