搜索
【题目】如图，O为矩形ABCD对角线的交点，DE∥AC，CE∥BD．
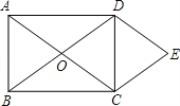
（1）试判断四边形OCED的形状，并说明理由；
（2）若AB=6，BC=8，求四边形OCED的面积．
参考答案：
【答案】（1）菱形；（2）24．
【解析】试题分析：（1）根据题意得出平行四边形，根据矩形的性质得出邻边相等，则判定为菱形；（2）连接OE，根据矩形和菱形的性质得出OE=BC=8，然后计算面积．
试题解析：（1）四边形OCED是菱形，
∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形，
在矩形ABCD中，OC=OD，
∴四边形OCED是菱形
（2）连结OE．由菱形OCED得：CD⊥OE，
∴OE∥BC
又CE∥BD，
∴四边形BCEO是平行四边形，
∴OE=BC=8，
∴S四边形OCED=
-
科目： 来源： 题型：
查看答案和解析>>【题目】代数式：①-x；②x2+x-1；③
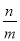；④
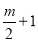；⑤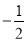
；⑥πm3y；⑦
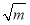；⑧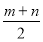
．（1）请上述代数式的序号分别填在相应的圆圈内：
（2）其中次数最高的多项式是__________次_________项式；
（3）其中次数最高的单项式的次数是____________，系数是____________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=
x+6的图象与x轴、y轴分别交于A、B两点，点C与点A关于y轴对称.动点P、Q分别在线段AC、AB上(点P与点A、C不重合），且满足∠BPQ=∠BAO。(1)求点A、 B的坐标及线段BC的长度；
(2)当点P在什么位置时，△APQ≌△CBP,说明理由；
(3)当△PQB为等腰三角形时，求点P的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】点P，Q在数轴上分别表示的数分别为p，q，我们把p，q之差的绝对值叫做点P，Q之间的距离，即
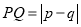．如图，在数轴上，点A，B，O，C，D的位置如图所示，则
；
；
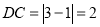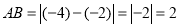．请探索下列问题：
（1）计算
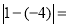____________，它表示哪两个点之间的距离？________________________．（2）点M为数轴上一点，它所表示的数为x，用含x的式子表示PB=____________；当PB=2时，x=____________；当x=____________时，|x+4|+|x-1|+|x-3|的值最小．
（3）|x-1|+|x-2|+|x-3|+…+|x-2018|+|x-2019|的最小值为________________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在菱形ABCD中，AB＝6，∠DAB＝60°，AE分别交BC、BD于点E、F，CE＝2，连接CF，以下结论：①△ABF≌△CBF；②点E到AB的距高是
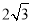；③AF＝CF；④△ABF的面积为
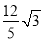其中一定成立的有( )个.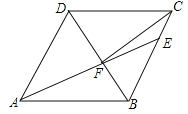
A. 1B. 2C. 3D. 4
-
科目： 来源： 题型：
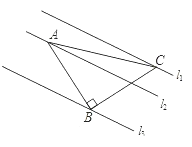
查看答案和解析>>【题目】如图，已知△ABC中，∠ABC＝90°，AB＝BC，三角形的顶点在相互平行的三条直线l1，l2，l3上，且l1、l2之间的距离为2，l2、l3之间的距离为3，则AC的长是_________；
-
科目： 来源： 题型：
查看答案和解析>>【题目】为充分发挥市场机制和价格杠杆在水资源配置中的作用，促进节约用水，提高用水效率，2017年7月1日起某地实行阶梯水价，价目如右表（注：水费按月结算，m3表示立方米）：例：某户居民5月份共用水23m3，则应缴水费3×18+4×(23-18)=74（元）．
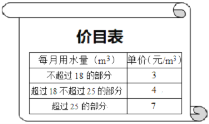
（1）若A居民家1月份共用水12m3，则应缴水费__________元；
（2）若B居民家2月份共缴水费66元，则用水__________m3；
（3）若C居民家3月份用水量为am3（a低于20m3，即a<20)，且C居民家3、4两个月用水量共40m3，求3、4两个月共缴水费多少元？（用含a的代数式表示，不要求化简）
（4）在（3）中，当a=19时，求C居民家3、4两个月共缴水费多少元？
相关试题
