Question

【题目】如图，在ABCD中，AM，CN分别是∠BAD和∠BCD的平分线，添加一个条件，仍无法判断四边形AMCN为菱形的是（ ）

A．AM=AN B．MN⊥AC

C．MN是∠AMC的平分线 D．∠BAD=120°

Answer 1

【答案】D.

【解析】

试题解析：如图，

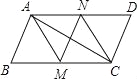
∵四边形ABCD是平行四边形，

∴∠B=∠D，∠DAB=∠DCB，AB=CD，AD=BC，

∵AM，CN分别是∠BAD和∠BCD的平分线，

∴∠DCN=∠DCB，∠BAM=∠BAD，

∴∠BAM=∠DCN，

在△ABM和△CDN中

，

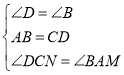∴△ABM≌△CDN（ASA），

∴AM=CN，BM=DN，

∵AD=BC，

∴AN=CM，

∴四边形AMCN是平行四边形，

A、∵四边形AMCN是平行四边形，AM=AN，

∴平行四边形AMCN是菱形，故本选项错误；

B、∵MN⊥AC，四边形AMCN是平行四边形，

∴平行四边形AMCN是菱形，故本选项错误；

C、∵四边形AECF是平行四边形，

∴AF∥BC，

∴∠FAC=∠ACE，

∵AC平分∠EAF，

∴∠FAC=∠EAC，

∴∠EAC=∠ECA，

∴AE=EC，

∵四边形AECF是平行四边形，

∴四边形AECF是菱形，故本选项错误；

D、根据∠BAD=120°和平行四边形AMCN不能推出四边形是菱形，故本选项正确；

故选D．