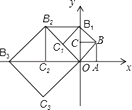
【题目】如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OBl为边作第三个正方形OBlB2C2,照此规律作下去,则点B2018的坐标为______.
参考答案:
【答案】(-21009,21009)
【解析】
首先求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标,找出这些坐标的之间的规律,然后根据规律计算出点B2018的坐标.
∵正方形OABC边长为1,
∴OB=![]() ,
,
∵正方形OBB1C1是正方形OABC的对角线OB为边,
∴OB1=2,
∴B1点坐标为(0,2),
同理可知OB2=2![]() ,B2点坐标为(2,2),
,B2点坐标为(2,2),
同理可知OB3=4,B3点坐标为(4,0),
B4点坐标为(4,4),B5点坐标为(0,8),
B6(8,8),B7(16,0).
B8(16,16),B9(0,32),
由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的![]() 倍,
倍,
∵2018÷8的商为252余2,
∴B2018的纵横坐标符号与点B2的相同,横坐标为负值,纵坐标是正值,
∴B2018的坐标为(-21009,21009).
故答案为:(-21009,21009).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图①,求证:OB∥AC.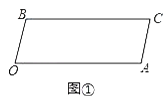
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.求∠EOC的度数.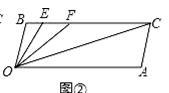
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.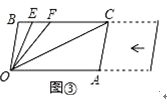
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.

(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)﹣24+(﹣16)﹣(﹣18)﹣13
(2)
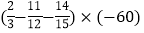
(3)﹣22÷(﹣4)3+|0.8﹣1|×
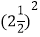
(4)99
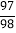 ×49
×49 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,已知点E(3,2)在双曲线y=
 (x>0)上。过动点P(t,0)作x轴的垂线分别与该双曲线和直线y=
(x>0)上。过动点P(t,0)作x轴的垂线分别与该双曲线和直线y= x交于A.、B两点,以线段AB为对角线作正方形ADBC,当正方形ADBC的边(不包括正方形顶点)经过点E时,则t的值为___.
x交于A.、B两点,以线段AB为对角线作正方形ADBC,当正方形ADBC的边(不包括正方形顶点)经过点E时,则t的值为___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列叙述中,不正确的个数有( ) ①所有的正数都是整数②|a|一定是正数 ③无限小数一定是无理数 ④(﹣2)3没有平方根 ⑤
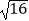 的平方根是±4 ⑥
的平方根是±4 ⑥ 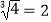 .
.
A.3个
B.4个
C.5个
D.6个 -
科目: 来源: 题型:
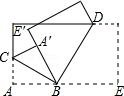
查看答案和解析>>【题目】如图,将一张长方形纸片的一角斜折过去,顶点A落在A′处,BC为折痕,再将BE翻折过去与BA′重合,BD为折痕,那么两条折痕的夹角∠CBD=度.
相关试题

