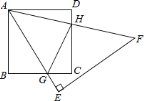
【题目】如图,正方形ABCD的面积为1cm2,△AEF为等腰直角三角形,∠E=90°,AE和BC交于点G,AF和CD交于点H,则△CGH的周长_________
参考答案:
【答案】2
【解析】
延长CB至M,使BM=DH,连接AM;先证明△ABM≌△ADH(SAS),得出AM=AH,∠BAM=∠DAH,证出∠MAG=∠HAG,再证明△AMB≌△AHG(SAS)得出GM=GH,即可求出结果.
延长CB至M,使BM=DH,连接AM;如图所示:
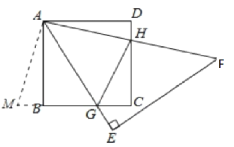
∵四边形ABCD是正方形,正方形ABCD的面积为1cm![]() ,
,
∴AB=BC=CD=1,∠BAD=∠ABC=∠D=90°,
∴∠ABM=90°,
在△ABM和△ADH中,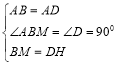 ,
,
∴△ABM≌△ADH(SAS),
∴AM=AH,∠BAM=∠DAH,
∵△AEF是等腰直角三角形,
∴∠HAG=45°,
∴∠BAG+∠DAH=45°,
∴∠MAG=45°,
在△AMG和△AHG中,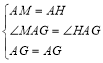 ,
,
∴△AMG≌△AHG(SAS),
∴GM=GH,
∴△CGH的周长=GH+CG+CH=GM+CG+CH
=BM+BG+CG+CH=DH+BG+CG+CH=BC+CD=2
故答案为:2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第12个图形中有全等三角形的对数是( )
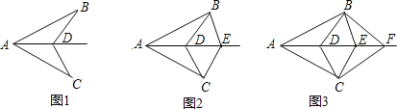
A. 80对B. 78对C. 76对D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,二次函数
 的图象的对称轴是直线x=1,且经过点(0,2).有下列结论:①ac>0;②
的图象的对称轴是直线x=1,且经过点(0,2).有下列结论:①ac>0;② ;③a+c<2-b;④
;③a+c<2-b;④ ; ⑤x=-5和x=7时函数值相等.其中正确的结论有 ( )
; ⑤x=-5和x=7时函数值相等.其中正确的结论有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校团委为积极参与“陶行知杯.全国书法大赛”现场决赛,向学校学生征集书画作品,今年3月份举行了“书画比赛”初赛,初赛成绩评定为A,B,C,D,E五个等级.该校七年级书法班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题.

(1)该校七年级书法班共有 名学生;扇形统计图中C等级所对应扇形的圆心角等于 度,并补全条形统计图;
(2)A等级的4名学生中有2名男生,2名女生,现从中任意选取2名学生参加“陶行知杯.全国书法大赛”现场决赛,请你用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知R t△ABC,∠ABC=90°,以直角边AB为直径作O,交斜边AC于点D,连结BD.
(1)若AB=3,BC=4,求边BD的长;
(2)取BC的中点E,连结ED,试证明ED与⊙O相切.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线
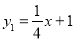 与
与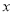 轴交于点
轴交于点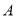 ,与
,与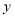 轴交于点
轴交于点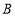 ,与反比例函
,与反比例函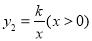 的图象交于点
的图象交于点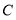 ,且
,且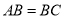 .
.(1)求点
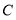 的坐标和反比例函数
的坐标和反比例函数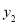 的解析式;
的解析式;(2)点
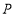 在
在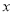 轴上,反比例函数
轴上,反比例函数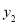 图象上存在点
图象上存在点 ,使得四边形
,使得四边形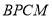 为平行四边形,求点M的坐标.
为平行四边形,求点M的坐标.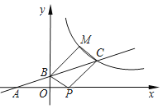
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料,回答问题:
解方程x4-5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2-5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;
当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=-1,x3=2,x4=-2.
在由原方程得到方程①的过程中,利用换元法达到降次的目的,体现了数学的转化思想,请利用上述方法解方程

相关试题

