【题目】如图,在正方形ABCD中,点E、F分别为边BC、CD上两点,∠EAF=45°, 过点A作∠GAB=∠FAD,且点G为边CB延长线上一点.①△GAB≌△FAD吗?说明理由。②若线段DF=4, BE=8,求线段EF的长度。③若DF=4,CF=8.求线段EF的长度。


参考答案:
【答案】(1)全等 (2)7 (3)EF=10
【解析】(1)、根据正方形的性质得出AB=AD,∠ABG=∠D,结合∠GAB=∠FAD得出三角形全等;(2)、根据三角形全等得出BG=DF=4,AG=AF,根据∠EAF=45°以及三角形全等、正方形的性质得出∠GAE=∠EAF,从而得出△GAE和△FAE全等,从而得出答案;(3)、根据第二题的结论得出答案.
(1)全等
证明:∵四边形ABCD为正方形, ∴AB=AD,∠ABG=∠D,
在△ABG和△ADF中 ∵∠GAB=∠FAD,AB=AD,∠ABG=∠D, ∴△GAB≌△FAD.
(2)解:∵∠BAD=90°,∠EAF=45°,∴∠DAF+∠BAE=45°,
∵△GAB≌△FAD, ∴∠GAB=∠FAD,AG=AF, ∴∠GAB+∠BAE=45°,∴∠GAE =45°,
∴∠GAE=∠EAF, 在△GAE和△FAE中,∵AG=AF, ∠GAE=∠EAF,AE=AE,
∴△GAE≌△FAE(SAS), ∴EF=GE, ∵△GAB≌△FAD,∴GB=DF,
∴EF=GE=GB+BE=FD+BE=3+4=7;
(3)EF=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为
为 的直径
的直径 延长线上的一点,
延长线上的一点, 与
与 相切,切点为
相切,切点为 ,点
,点 是
是 上一点,连接
上一点,连接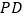 .已知
.已知 .下列结论:
.下列结论: 与
与 相切;
相切; 四边形
四边形 是菱形;
是菱形; ;
; .
.其中正确的个数为( )

A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象与y=x-1的图象平行,且经过点(2,6).
(1)求一次函数y=kx+b的表达式.
(2)求这个一次函数y=kx+b与坐标轴的两个交点坐标,并在直角坐标系中画出这个函数的图象.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 是
是 上一点,以
上一点,以 为圆心
为圆心 为半径的圆与
为半径的圆与 交于点
交于点 ,与
,与 交于点
交于点 ,连接
,连接 、
、 、
、 ,且
,且 .
. 求证:
求证: 是
是 的切线;
的切线; 若
若 ,求
,求 的半径.
的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,且CF⊥AD于H,下列判断,①BG是△ABD中边AD上的中线;②AD既是△ABC中∠BAC的角平分线,也是△ABE中∠BAE的角平分线;③CH既是△ACD中AD边上的高线,也是△ACH中AH边上的高线,其中正确的个数是( )
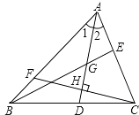
A.0B.1C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点D,E分别是△ABC的边BA和BC延长线上的点,作∠DAC的平分线AF,若AF∥BC.

(1)求证:△ABC是等腰三角形;
(2)作∠ACE的平分线交AF于点G,若∠B=40°,求∠AGC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
相关试题

