【题目】如图,已知点D,E分别是△ABC的边BA和BC延长线上的点,作∠DAC的平分线AF,若AF∥BC.

(1)求证:△ABC是等腰三角形;
(2)作∠ACE的平分线交AF于点G,若∠B=40°,求∠AGC的度数.
参考答案:
【答案】(1)证明见解析;(2)70°
【解析】
(1)根据AF平分∠DAC得出∠DAF=∠CAF,再根据AF∥BC求得∠DAF=∠B,∠CAF=∠ACB则可证明△ABC是等腰三角形;(2)根据AB=AC,∠B=40°,可求出∠ACE的角度,再根据CG平分∠ACE求出![]() ,则利用AF∥BC求出∠AGC的度数.
,则利用AF∥BC求出∠AGC的度数.
(1)证明:∵AF平分∠DAC,
∴∠DAF=∠CAF,
∵AF∥BC,
∴∠DAF=∠B,∠CAF=∠ACB,
∴∠B=∠ACB,
∴△ABC是等腰三角形;
(2)解:∵AB=AC,∠B=40°,
∴∠ACB=∠B=40°,
∴∠BAC=100°,
∴∠ACE=∠BAC+∠B=140°,
∵CG平分∠ACE,
∴![]() ACE=70°,
ACE=70°,
∵AF∥BC,
∴∠AGC=180°﹣∠BCG=70°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 是
是 上一点,以
上一点,以 为圆心
为圆心 为半径的圆与
为半径的圆与 交于点
交于点 ,与
,与 交于点
交于点 ,连接
,连接 、
、 、
、 ,且
,且 .
. 求证:
求证: 是
是 的切线;
的切线; 若
若 ,求
,求 的半径.
的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E、F分别为边BC、CD上两点,∠EAF=45°, 过点A作∠GAB=∠FAD,且点G为边CB延长线上一点.①△GAB≌△FAD吗?说明理由。②若线段DF=4, BE=8,求线段EF的长度。③若DF=4,CF=8.求线段EF的长度。


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,且CF⊥AD于H,下列判断,①BG是△ABD中边AD上的中线;②AD既是△ABC中∠BAC的角平分线,也是△ABE中∠BAE的角平分线;③CH既是△ACD中AD边上的高线,也是△ACH中AH边上的高线,其中正确的个数是( )
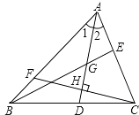
A.0B.1C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ABD,还应补充一个条件,才能推出△ABC≌△ABD.补充下列其中一个条件后,不一定能推出△ABC≌△ABD的是( )

A. BC=BD B. AC=AD C. ∠ACB=∠ADB D. ∠CAB=∠DAB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:
 ≈2.449,结果保留整数)
≈2.449,结果保留整数)
相关试题

