【题目】A、B两站间的路程为448千米,一列慢车从A站出发,每小时行驶60千米;一列快车从B站出发,每小时行驶80千米,问:
(1)两车同时开出,相向而行,出发后多少小时相遇?
(2)两车相向而行,慢车先开出28分钟,快车开出后多少小时两车相遇?
参考答案:
【答案】(1)3.2小时;(2)3小时.
【解析】
试题分析:(1)设出发后x小时两车相遇,则慢车行驶的路程为60x千米,快车行驶的路程为80x千米,由慢车行驶的路程+快车行驶的路程=448km建立方程求出其解即可;(2)设快车开出y小时后两车相遇,则快车行驶的路程为80y千米,慢车行驶的路程为60(y+![]() )千米.由慢车行驶的路程+快车行驶的路程=448km建立方程求出其解即可.
)千米.由慢车行驶的路程+快车行驶的路程=448km建立方程求出其解即可.
试题解析:(1)设x小时后两车相遇,根据题意得:60x+80x=448,解得 x=3.2小时,答:两车同时开出,相向而行,出发后3.2小时相遇;
(2)设快车开出y小时后两车相遇,根据题意得:60(![]() +y)+80y=448,解得y=3小时,答:快车开出后3小时两车相遇.
+y)+80y=448,解得y=3小时,答:快车开出后3小时两车相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为4cm的等边三角形,AD为BC边上的高,点P沿BC向终点C运动,速度为1cm/s,点Q沿CA、AB向终点B运动,速度为2cm/s,若点P、Q两点同时出发,设它们的运动时间为x(s).
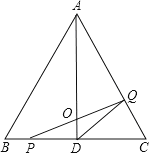
(l)求x为何值时,PQ⊥AC;x为何值时,PQ⊥AB?
(2)当O<x<2时,AD是否能平分△PQD的面积?若能,说出理由;
(3)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围(不要求写出过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下图,每个小正方形的边长均为1,可以得到每个小正方形的面积为1.
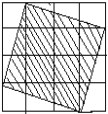
(1)图中阴影部分的面积是多少? 阴影部分正方形的边长是多少?
(2)估计边长的值在哪两个整数之间?
(3)请你利用图形在数轴上用刻度尺和圆规表示阴影部分正方形边长所表示的数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在学习了统计知识后,就下表所列的5种用牙不良习惯对全班每一个同学进行了问卷调查(每个被调查的同学必须选择而且只能在5种用牙不良习惯中选择一项),调查结果如下统计图所示.根据以上统计图提供的信息,回答下列问题:
种类
A
B
C
D
E
不良习惯
睡前吃水果喝牛奶
用牙开瓶盖
常喝饮料嚼冰
常吃生冷零食
磨牙
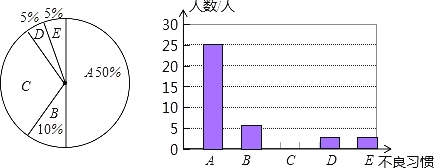
(1)这个班有多少名学生?
(2)这个班中有C类用牙不良习惯的学生多少人?占全班人数的百分比是多少?
(3)请补全条形统计图;
(4)根据调查结果,估计这个年级850名学生中有B类用牙不良习惯的学生多少人?
-
科目: 来源: 题型:
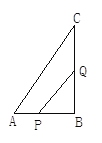
查看答案和解析>>【题目】如图所示的Rt△ABC中,∠B=90°,点P从点B开始沿BA边以1厘米/秒的速度向点A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为35平方厘米?PQ的距离是多少厘米?(结果用最简二次根式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。AF平分∠CAB,交CD于点E,交CB于点F。
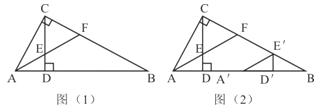
(1)求证:CE=CF。
(2)将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图(2)所示。试猜想:BE′与CF有怎样的数量关系?请证明你的结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌
粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价
 (元)之间的函数关系式;(4分)
(元)之间的函数关系式;(4分)(2)当每盒售价定为多少元时,每天销售的利润
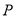 (元)最大?最大利润是多少?(6分)
(元)最大?最大利润是多少?(6分)
相关试题

