搜索
【题目】某校开展“校园献爱心”活动.准备向西部山区学校捐赠男、女两种款式的书包，已知男款书包单价
元/个，女款书包单价
元/个.
原计划募捐
元，恰好可购买两种款式的书包
个，问两种款式的书包各买多少个？
在捐款活动中，师生积极性高，实际捐款额和书包数量都高于原计划.快递公司将这些书包装箱运送，其中每箱书包数量相同.第一次他们领走这批的
，结果装了
箱还多
个书包；第二次他们把余下的
领走.连同第一次装箱剩下的个书包一起，刚好装了
箱.问:实际购买书包共多少个？
参考答案：
【答案】（1）购买男款书包
个，则购买女款书包
个；（2）实际购买书包共
个.
【解析】
（1）设购买男款书包
个，从而可得购买女款书包的个数，再根据募捐总金额建立方程求解即可；
（2）设实际购买书包共
个，根据两次装箱时“每箱书包数量相同”建立方程求解即可.
（1）设购买男款书包个，则购买女款书包
个
依题意得：
解得:
则
(个)
答:购买男款书包个，则购买女款书包个；
（2）设实际购买书包共个
依题意得:
解得:
答:实际购买书包共个.
-
科目： 来源： 题型：
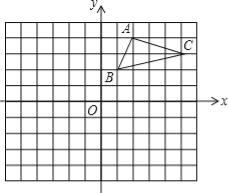
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：
（1）画出△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标．
（2）画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2，并写出点A2的坐标．
【答案】（1）作图见解析；点A1的坐标（2，﹣4）；（2）作图见解析；点A2的坐标（﹣2，4）．
【解析】
试题分析：（1）分别找出A、B、C三点关于x轴的对称点，再顺次连接，然后根据图形写出A点坐标；
（2）将△A1B1C1中的各点A1、B1、C1绕原点O旋转180°后，得到相应的对应点A2、B2、C2，连接各对应点即得△A2B2C2．
试题解析：（1）如图所示：点A1的坐标（2，﹣4）；
（2）如图所示，点A2的坐标（﹣2，4）．
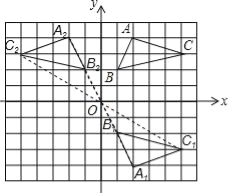
考点：1.作图-旋转变换；2.作图-轴对称变换．
【题型】解答题
【结束】
18【题目】观察下面的点阵图和相应的等式，探究其中的规律：
（1）认真观察，并在④后面的横线上写出相应的等式．
①1=1 ②1+2=
=3 ③1+2+3=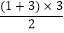
=6 ④ …（2）结合（1）观察下列点阵图，并在⑤后面的横线上写出相应的等式．
1=12②1+3=22③3+6=32④6+10=42⑤ …
（3）通过猜想，写出（2）中与第n个点阵相对应的等式 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知两个多项式A=9xy＋7xy－x－2,B=3xy－5xy＋x＋7
（1）求A－3B;
（2）若要使A－3B的值与x的取值无关，试求y的值；
-
科目： 来源： 题型：
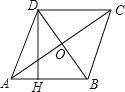
查看答案和解析>>【题目】如图，四边形ABCD是菱形，对角线AC和BD相交于点O，AC=8cm，BD=6cm，DH⊥AB于H．
（1）求菱形ABCD的面积；
（2）求DH的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一副三角板按如图1方式拼接在一起，其中边
，
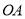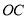与直线
重合，
，
．
（1）图 1 中，
=______°．（2）如图2，三角板
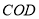固定不动，将三角板
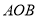绕点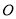
按顺时针方向旋转一个角度
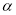，在转动过程中两块三角板都在直线的上方： ①当
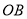平分、、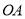
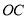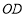其中的两边组成的角时，求满足要求的所有旋转角度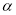的值；②是否存在
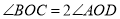？若存在，求此时的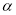的值；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】植树节来临之际，学校准备购进一批树苗，已知2棵甲种树苗和5棵乙种树苗共需113元；3棵甲种树苗和2棵乙种树苗共需87元．
（1）求一棵甲种树苗和一棵乙种树苗的售价各是多少元？
（2）学校准备购进这两种树苗共100棵，并且乙种树苗的数量不多于甲种树苗数量的2倍，请设计出最省钱的购买方案，并求出此时的总费用．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）观察猜想：
在Rt△ABC中，∠BAC=90°，AB=AC，点D在边BC上，连接AD，把△ABD绕点A逆时针旋转90°，点D落在点E处，如图①所示，则线段CE和线段BD的数量关系是 ，位置关系是 ．
（2）探究证明：
在（1）的条件下，若点D在线段BC的延长线上，请判断（1）中结论是还成立吗？请在图②中画出图形，并证明你的判断．
（3）拓展延伸：
如图③，∠BAC≠90°，若AB≠AC，∠ACB=45°，AC=
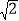，其他条件不变，过点D作DF⊥AD交CE于点F，请直接写出线段CF长度的最大值．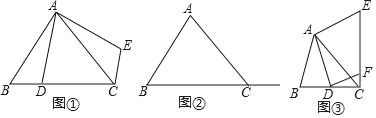
相关试题
