【题目】已知,在□ABCD中,连接对角线![]() ,
, ![]() 平分线
平分线![]() 交
交![]() 于点
于点![]() ,
, ![]() 平分线
平分线![]() 交
交![]() 于点
于点![]() ,
, ![]() 、
、![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 上一点,且
上一点,且![]() 。
。
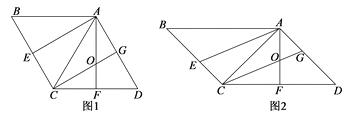
(1)如图1,若![]() 是等边三角形,
是等边三角形, ![]() ,求□ABCD的面积;
,求□ABCD的面积;
(2)如图2,若![]() 是等腰直角三角形,
是等腰直角三角形, ![]() ,求证:
,求证: ![]() 。
。
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据平行四边形ABCD的面积=2×SΔACD,求出ΔACD的面积即可;
(2)如图2中,延长OF到M,使得FM=OF,连接CM.只要证明AC=AM,OA=AG=CE即可解决问题.
试题解析:(1)如图1中,
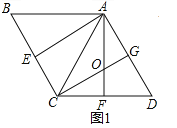
∵△ACD是等边三角形,
∴AC=CD=AD,∠ACD=∠D=∠CAD=60°,
∵∠OAC=∠OCA=30°,
∴OA=OC=2,
∵CG平分∠ACD,
∴CG⊥AD,
在RtΔAOG中,∵∠OAG=30°OA=2,
∴OG=![]() OA=1,AG=
OA=1,AG= ![]() ,
,
∴AD=2AG=2![]() ,
,
∴S△ACD=![]() ADCG=
ADCG=![]() =3
=3![]() .
.
∴平行四边形ABCD的面积=2S△ACD=6![]() .
.
(2)如图2中,延长OF到M,使得FM=OF,连接CM.
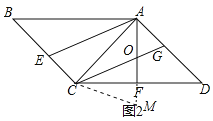
∵△ACD是等腰直角三角形,AF、CG是角平分线,
∴AF⊥CF,∠OAC=∠D=∠ACD=45°,∠OCA=∠DCG=22.5°,
∴∠OCF=∠OAC+∠OCA=67.5°,∠AGD=∠D+∠GCD=67.5°,
∴∠AOG=∠AGO,
∴OA=AG,
∵CF⊥OM,OF=OM,
∴CO=CM,
∴∠M=∠COM=67.5°,
∴∠ACM=180°﹣∠CAM﹣∠M=67.5°,
∴∠CAM=∠M,
∴CA=AM,
∵∠BAE=∠GCD=22.°5,AB∥CD,
∴∠BAC=∠ACD=45°,
∴∠EAC=∠ACG=22.5°,
∴AE∥CG,∵EC∥AG,
∴四边形AECG是平行四边形,
∴CE=AG=OA,
∴AC=AM=OA+OM=CE+2OF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42
B.32
C.42 或 32
D.37 或 33 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程3xm-13yn=7x是二元一次方程,则m+n=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A、B是抛物线y=ax2(a>0)上两点.若点A、B的坐标分别为(3,m)、(4,n),则m_____n.(填“>”、“=”或“<”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于空气污染,气候干旱等因素,今年流感大肆流行,根据山东省卫计委统计,截止2018年1月,本年度全省共报告流感样病例442000例,其中0﹣14岁年龄组占到总病例数的88.09%,用科学记数法表示数字442000是( )
A. 4.42×103 B. 442×103 C. 4.42×105 D. 442×105
-
科目: 来源: 题型:
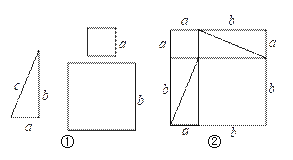
查看答案和解析>>【题目】如图①是1个直角三角形和2个小正方形,直角三角形的三条边长分别是a、b、c,其中a、b是直角边.2个小正方形的边长分别是a、b.
(1)将4个完全一样的直角三角形和2个小正方形构成一个大正方形(如图②).用两种不同的方法列代数式表示图②中的大正方形面积:方法一:_______;方法二:_____;
(2)观察图②,试写出(a+b)2,a2,2ab,b2这四个代数式之间的等量关系,为___ ____;
(3)利用你发现的结论,求:9922+16×992+64的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【探索新知】
如图1,点C将线段AB分成AC和BC两部分,若BC=
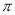 AC,则称点C是线段AB的圆周率点,线段AC、BC称作互为圆周率伴侣线段.
AC,则称点C是线段AB的圆周率点,线段AC、BC称作互为圆周率伴侣线段.(1)若AC=3,则AB=_____;
(2)若点D也是图1中线段AB的圆周率点(不同于C点),则AC_____DB;(填“=”或“≠”)
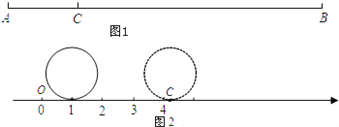
【深入研究】
如图2,现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1的点重合,并把圆片沿数轴向右无滑动地滚动1周,该点到达点C的位置.
(3)若点M、N均为线段OC的圆周率点,求线段MN的长度.
相关试题

